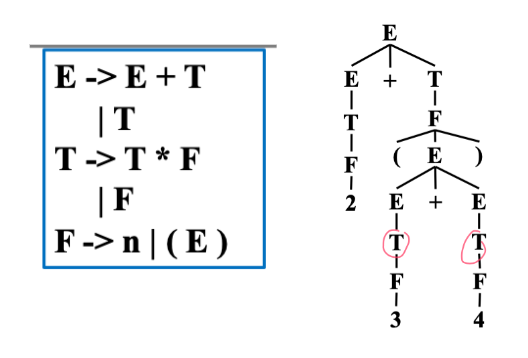
Semantic Analysis | Activation Record👀

约 7081 个字 211 行代码预计阅读时间 26 分钟

过渡知识👀

属性文法 | Attribute Grammar👀

Warning

龙书对此讲解十分详细，本课基于虎书了解概念即可，基本思想 就是给一些语义规则赋予一些含义

属性文法：上下文无关文法 + 属性 + 属性计算规则
- 属性：描述文法符号的语义特征，如变量的类型、值等。例，非终结符 $E$ 的属性 $E\text{.val}$ 表示 $E$ 的值
- 属性计算规则 (语义规则)：与产生式相关联、反映文法符号属性之间关系的规则，比如“如何计算 $E\text{.val}$”
属性计算规则: 仅表明属性间“抽象”关系，不涉及具体实现细节，如计算次序等

用属性描述语义信息，用语义规则描述属性之间的关系，将语义规则与语法规则相结合

属性文法的潜在应用大体分为两类（但由于各种局限性，属性文法并未得到普及）

“推导类” 应用：类似程序分析
- 表达式的类型、值、执行代价等
“生成类” 应用：类似程序合成
- 抽象语法树生成
- 中间代码甚至汇编生成

属性文法的实现

可通过 Parser 生成器支持的“语义动作” (Semantic action) 实现计算, 并应用于抽象语法树生成等场景

本课只需要关注 Yacc, Bison 中的 Semantic Action，以及怎么生成 AST 这些具体应用即可

Semantic Action👀

每个终结符和非终结符都可以与自己的语义值 (semantic value) 的类型相关联 (给每一个符号绑定一个语义值，比如类型，数学值等)

CFG and its Semantic Action

Suppose that we want to “evaluate” the values of an expression：

E -> E1 + T {E.val = E1.val + T.val}
E -> E1 - T {E.val = E1.val - T.val}
E -> T      {E.val = T.val}
T -> (E)    {T.val = E.val}
T -> num    {T.val = num.val}

在递归下降分析中：
- 语义动作指代 parsing 函数的返回值，或这些函数的 side effect, 又或者两者皆有
- For each terminal and nonterminal symbol, we associate a type of semantic values representing phrases derived from that symbol.
Example

T -> T * F 对应的 semantic action:
```
int a = T();
eat(TIMES);
int b = F();
return a * b;
```
又比如在 Yacc 中加入 Semantic Action, 从而可以一边解析一边计算表达式的值
- {...}: semantic action, 可以是任意合法的 C 代码
- $i: the semantic values of the i-th RHS symbol
- $$: the semantic value of the LHS nonterminal symbol
- %union: difference possible types for semantic values to carry
- <variant>: declares the type of each terminal and nonterminal
Example
```
%{ ... %}
%union {
    int num;
    string id;
}
%token <num> INT
%token <id> ID
%type <num> exp
...
%left UMINUS
%%
exp : INT {$$ = $1;}
    | exp '+' exp {$$ = $1 + $3;}
    | exp '-' exp {$$ = $1 - $3;}
    | exp '*' exp {$$ = $1 * $3;}
    | MINUS exp %prec UMINUS {$$ = -$2;}
```

Semantic Actions in Yacc-Generated Parsers

Yacc 生成的 parser 会保留一个与状态栈平行的值栈，用于存储语义值
当 parser 规约一个产生式时，会执行相应的 semantic action，将计算结果压入值栈
当 parser 从符号栈中弹出 $Y_k, \dots Y_1$ 并弹入 $A$ 时, 也会从语义值栈中弹出 $k$ 个值, 并推入 semantic action 的结果

Abstract Parse Tree👀

考虑之前的 semantic action, 其实可以用 Yacc 和相应的 semantic action 写出一个完整的编译器

但是这样的编译器难以阅读和维护；
并且必须完全按照程序解析的顺序分析程序

由此，希望 separate issues of syntax (parsing) from issues of semantics (type-checking and translation to machine code)

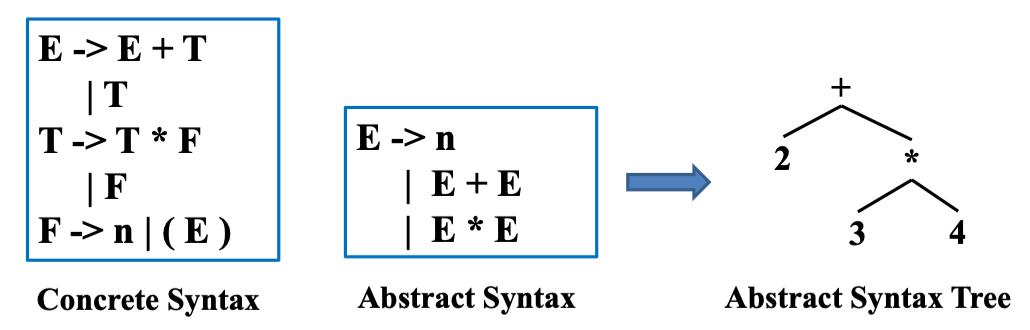
其中一个解决方案是：将语法树的构造与语义动作分离，即先构造语法树，再对语法树进行语义分析

Why we need AST

对于先前的语法树，他对输入的每一个 token 都有一个叶子节点，且每一个 parse 过程中的规约语法都有一个内部节点
这样的语法树被称为 concrete parse tree，它包含了所有的细节
但是这样的语法树不便于直接使用
- redundant and useless tokens for later phases
- depends too much on the grammar

Example

例如图中的 $T$ 可能只是之前为了消除二义性，临时加的新的 nonterminal，对于后续的语义分析是没有意义的

AST 所做的是在 parser 和编译器的后续阶段之间建立一个 clean interface (具体操作是 parser 使用 concrete syntax 为抽象语法建立语法树)

The semantic analysis phase takes this abstract syntax tree.

AST 的构造可以手写，也可以通过 parser generator 生成

manmade AST

A typedef for each nonterminal, a union-variant for each production.

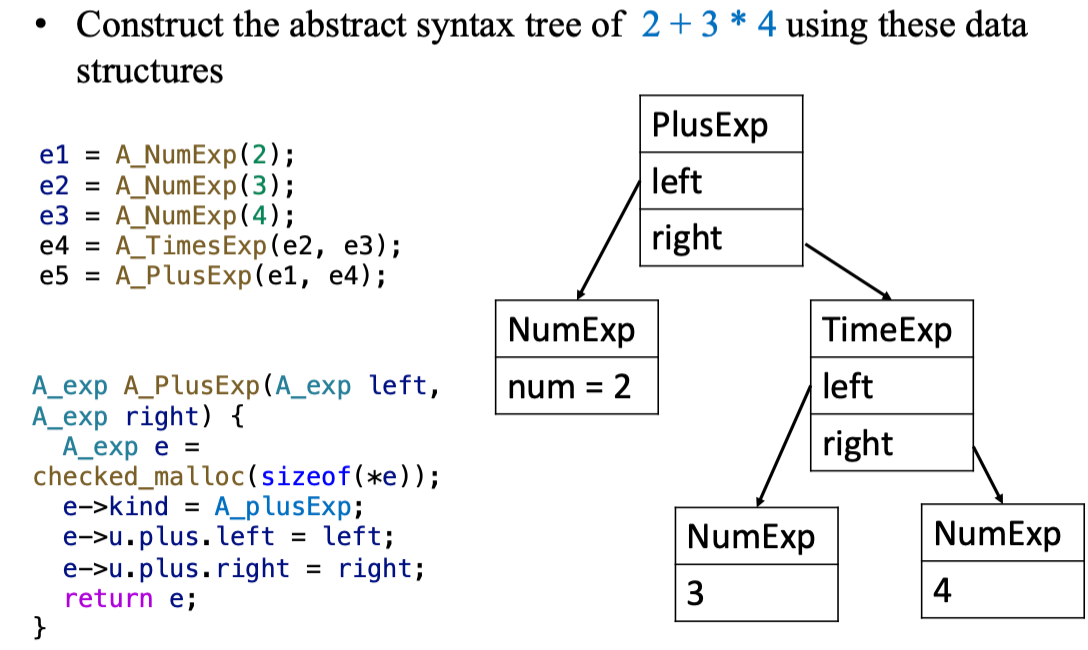
Example

对于文法：

E  -> n
    | E + E
    | E * E

使用如下数据结构表示 AST:

typedef struct A_exp_ *A_exp;
struct A_exp_ {
    enum {A_numExp, A_plusExp, A_timesExp} kind; 
    union {
        int num; 
        struct {A_exp left; A_exp right;} plus; 
        struct {A_exp left; A_exp right;} times; 
    } u; 
};

A_exp A_NumExp(int num);
A_exp A_PlusExp(A_exp left, A_exp right); 
A_exp A_TimesExp(A_exp left, A_exp right);

Building AST Automatically

    %{ ... %}
    %union {
        int num;
        string id;
    }
    %token <num> INT
    %token <id> ID
    %type <num> exp
    ...
    %left UMINUS
    %%
    exp : INT {$$ = $1;}
        | exp '+' exp {$$ = $1 + $3;}
        | exp '-' exp {$$ = $1 - $3;}
        | exp '*' exp {$$ = $1 * $3;}
        | MINUS exp %prec UMINUS {$$ = -$2;}

Applications of AST Traversals

Pretty print
Desugaring
Inlining
High-level optimizations (e.g., 删除公共子表达式)
Symbolic execution!(e.g., Clang Static Analyzer)
Semantic analysis , e.g., type checking
Translation to intermediate representations
…

Tiger Language👀

Simple control constructs:
- if-then, if-then-else
- while-loops, for-loops
- function calls
Two basic types: int and string
- Facility to define record and array types
- Facility to define mutually-recursive types
Supports nested functions, mutually recursive functions

1) Let-In-End Expressions

A Tiger program is expression (无 statement)

let
    <type declarations>
    <variable declarations>
    <function declarations>
in
    <sequence of expressions, separated by ;>
end

Scope extends to end of expression sequence

2) Type Declarations

Array lengths are not specified until creation

type t1 = int
type t2 = string
type rec1 = {f1:int, f2:t2}
type intArray = array of int

3) Variable Declarations

4) Function Declarations

Parameters are passed by value:

function add1(x:int):int = x+1;
function changeRec(r:rec1) =
    (r.f1 := r.f1 + 10; r.f2 := "hello")

Function declarations can be nested
- Nested functions can access local variables or parameters of outer functions

function f1(y:int):int =
let
    var z := 0
    var w := 0
    function f2():int = z + w * y
in
    f2()
end

5) Mutual Recursion

Functions and types can be mutually recursive

Mutually-recusive types must be declared consecutively with no intervening variable or function declarations | 互斥类型必须连续声明，中间不得有变量或函数声明
Each recursion cycle in a type definition must pass through a record or array type | 每个递归循环在类型定义中必须通过记录或数组类型
Mutually-recursive functions must be declared consecutively with no intervening type or variable declarations | 互斥递归函数必须连续声明，中间不得有类型或变量声明

Semantic Analysis👀

对编译器来说，单单词法和语法分析是不足的, 例如：

Does the dimension of a reference match the declaration?
Is an array access out of bound?
Where should a variable be stored (heap, stack,…)
…

上述问题的限制来源于语法分析的局限性，这些错误是否能检查出是依赖于值的，而不是语法

广义的 Semantic Analysis:

We need to analyze the semantics of programs
- Usually, this is done by traversing/analyzing various program representations
- Examples of representations: AST, control flow graph (CFG), program dependence graph (PDG), value flow graph (VFG), SSA (single static assignment).
Sample semantic analysis: type checking, code generation, dead code elimination, register allocation, etc

狭义的 Semantic Analysis:

语法分析检查不到的一些问题，用语义分析可以检查出来

本课程默认的语义分析：

Determine some static properties of program via AST, e.g.,
- Scope and visibility of names
  - every variable is declared before use
- Types of variables, functions, and expression
  - every expression has a proper type
  - function calls conform to definitions
Translate the AST into some intermediate code

Symbol Table👀

管理不同符号信息，比如某个变量在哪里可以使用、区分变量作用域

1) Binding: give a symbol a meaning | 把一些标志符绑定到有特定含义的属性,使用 $\mapsto$ 表示

E.g.,

Name/Symbol	Meaning/Attribute
type identifier	type (e.g., int , string)
variable identifier	type, value, access info, …
function identifier	argument types, return type, …

2) Environment: a set of bindings | 一组绑定

E.g., {$g \mapsto \text{string}, ~ a \mapsto \text{int}$}

3) Symbol table: the implementation of environment

Semantic analysis: traverse the abstract syntax tree (AST) in certain order while maintaining a symbol table

Example

考试可能考画 tiger 语言的符号表

function f(a:int, b:int, c:int) =
    (print_int(a+c) ;
    let var j := a+b
        var a := "hello"
    in print(a); print_int(j)
    end;
    print_int(b)
    )

假设最开始的 environment 是 $\sigma_0$
在第一行，函数定义建立新的 environment $\sigma_1$
- $\sigma_1 = \sigma_0 + \{a \mapsto \text{int},~ b \mapsto \text{int}, ~ c \mapsto \text{int}\}$
- 在第二行，标识符 $a, c$ 可以在环境 $\sigma_1$ 中查询到
在第三行，建立新的 environment $\sigma_2$
- $\sigma_2 = \sigma_1 + \{j \mapsto \text{int}\}$
在第四行，有 $\sigma_3 = \sigma_2 + \{a \mapsto \text{string}\}$
在第六行，As the semantic analysis reaches the end of each scope, the identifier bindings local to that scope are discarded.
- $\sigma_2, \sigma_3$ 都会被丢弃，environment 恢复为 $\sigma_1$

约定

Bindings in the right-hand table override those in the left

例如对上述 $\sigma_3$, $\sigma_2$ 中包含了 $a \mapsto \text{int}$
对于 $\sigma_3$, $\{a \mapsto \text{string}\}$ 会覆盖 $\sigma_2$ 中 $a$ 的 binding

Symbol Table 需实现的接口

insert: 将名称绑定到相关信息(如类型), 如果名称已在符号表中定义，则 新的绑定优先于旧的绑定
lookup: 在符号表中查找名称，以找到名称绑定的信息
beginScope: 进入一个新的作用域
endScope: 退出作用域，将符号表恢复到进入之前的状态

下面介绍 Efficient Implementation

两种实现风格

Imperative style (有了新环境就看不到旧环境，但退出作用域的时候还能返回到旧环境)
- 直到 $\sigma_1$ 变为 $\sigma_2$ 才修改 $\sigma_1$
- $\sigma_2$ 存在的时候，不可以访问 $\sigma_1$
- 处理完 $\sigma_2$ 后，我们可以撤销修改，返回到环境 $\sigma_1$
Functional style (每次变化都保存着旧环境)
- 创建环境 $\sigma_2$ 的同时，保存着 $\sigma_1$ 的原始状态
- 易于恢复到旧环境，但是需要更多的空间

Imperative Symbol Tables👀

Problem 1

ProblemSolution

如何做到高效的 lookup?

使用 hash table
E.g., $\sigma_{new} = \sigma + \{a \mapsto \text{int}\}$
那么就将 <a, int> 插入到 hash table 中

Problem 2

ProblemSolution

如何删除并恢复旧环境?

使用带有外部链 (external chaining) 的 hash table
E.g.: hash(a) -> <a, int> -> <a, string>

由此，我们可以设计一个 efficient imperative symbol table, 其中包含：

Hash Tables: an array of buckets
Bucket: list of entries (each entry maps identifier to binding)

具体的函数设计思想：

LookupInsertRestore

lookup entry for identifier key in symbol table:

Apply hash function to key for getting array element index
Traverse bucket in table[index] to find the binding. (table[x]: all entries whose keys hash to x)

Insert new element at front of bucket

strong update, 要么插入，要么覆盖
考虑 $\sigma + \{a \mapsto \tau 2\}$, 且 $\sigma$ 中已经含有 $\{a \mapsto \tau 1\}$
插入函数会保存 $\{a \mapsto \tau 1\}$，并将 $\{a \mapsto \tau 2\}$ 插入在表的更前面
- E.g., hash(a) -> <a, τ2> -> <a, τ1>

pop items off items at front of bucket.

考虑 $\sigma + \{a \mapsto \tau 2\}$, 且 $\sigma$ 中已经含有 $\{a \mapsto \tau 1\}$
当在 a 的作用域的结尾处完成 pop(a) 后，$\sigma$ 就被恢复了
- E.g. hash(a) -> <a, τ2> -> <a, τ1> 变为 hash(a) -> <a, τ1>

Warning

为了处理不同 scope, 还需其他辅助信息，比如指导 “需要 pop 几次”

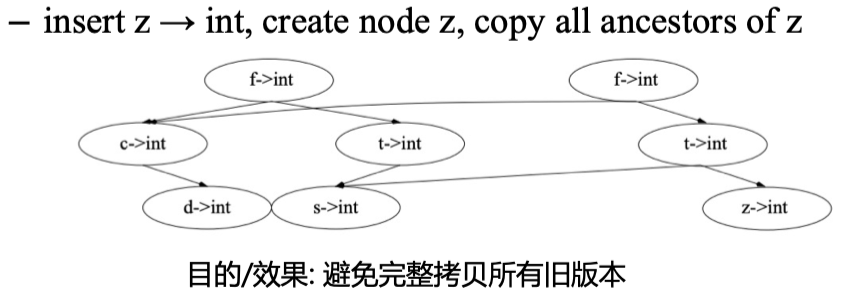
Functional Symbol Tables👀

Basic Idea

当实现环境 $\sigma_2$ ($\sigma_2 = \sigma_1 + \{a \mapsto \text{int}\}$) 时
创建一个新的表 $\sigma_2$，而不是修改 $\sigma_1$
但删除，回退时，我们可以直接返回到 $\sigma_1$

实现方式是：binary search trees (BSTs)

Each node contains mapping from identifier (key) to binding.
Use string comparison for “less than” ordering.
对于节点 $l$, 它的左子树 $L$, 右子树 $R$ 满足：
- 对于所有 $n \in L$, key(n) < key(l)
- 对于所有 $n \in R$, key(n) >= key(l)

用先前 efficient impressive 的方式也能实现，但是不够高效

LookupInsert

O(logn) for a balanced tree of n nodes

Copy the nodes from the root to the parent of the inserted node

Summary

Imperative Style : (side effects)
- When beginning-of-scope entered, entries added to table using side-effects. (old table destroyed)
- When end-of-scope reached, auxiliary info used to remove previous additions. (old table reconstructed)
Functional Style : (no side effects)
- When beginning-of-scope entered, new environment created by adding to old one, but old table remains intact
- When end-of-scope reached, retrieve old table.

它们对 lookup, insert, beginScope, endScope 等接口的支持，复杂度上各有优势

Symbols in the Tiger Compiler👀

实现表的时候存在一个问题：对于判断 key value = string | (strcmp), 我们在查找的时候需要进行大量的字符串比较操作

一种解决方法是：使用 symbol 数据结构代替

即每个 symbol 对象都与整数值相关联
相同的字符串映射到同一个 symbol 对象
于是之前比较 key value = symbol 可以变成简单的整数比较

Implementation of Symbol Tables👀

The interface of symbols and symbol tables:

void*: 在编译器中为不同目的使用不同的绑定概念, e.g.,
- Type binding for types
- value binding for variables and functions

typedef struct S_symbol_ *S_symbol;
S_symbol S_Symbol(string name);
string S_name(S_symbol s);

typedef struct TAB_table_ *S_table;
S_table S_empty(void);
void S_enter(S_table t, S_symbol sym, void *value);
void *S_look(S_table t, S_symbol sym);
void S_beginScope(S_table t);
void S_endScope(S_table t);

mksymbol, S_Symbol, S_name

static S_symbol mksymbol(string name, S_symbol next) {
    S_symbol s = checked_malloc(sizeof(*s));
    s->name = name;
    s->next = next;
    return s;
}

S_symbol S_Symbol(string name) {
    int index = hash(name) % SIZE;
    S_symbol syms = hashtable[index], sym;
    for (sym = syms; sym; sym = sym->next)
        if (strcmp(sym->name, name) == 0)
            return sym;
    sym = mksymbol(name, syms);
    hashtable[index] = sym;
    return sym;
}

string S_name(S_symbol s) {
    return s->name;
}

用 C 语言实现的 Tiger 编译器使用 destructive update 的方式来更新 environments
An imperative table is implemented using a hash table.

S_empty, S_enter, S_look

S_table S_empty(void) {
    return TAB_empty();
}

void S_enter(S_table t, S_symbol sym, void *value) {
    TAB_enter(t, sym, value);
}

void *S_look(S_table t, S_symbol sym) {
    return TAB_look(t, sym);
}

For destructive-update environments, 通过下面的方式实现 beginScope 和 endScope:

S_beginScope: 记住表格的当前状态；
S_endScope: 将表恢复到最近一次 beginScope 的位置。

S_beginScope, S_endScope

static struct S_symbol_ marksym = { “<mark>”, 0 };
void S_beginScope(S_table t) {
    S_enter(t, &marksym, NULL);
}

void S_endScope(S_table t) {
    S_symbol s;
    do
        s = TAB_pop(t);
    while (s != &marksym);
}

Auxiliary stack:

Showing in what order the symbols were “pushed” into the symbol table. | 显示符号表中符号的顺序
As each symbol is popped, the head binding in its bucket is removed. ｜每次弹出一个符号，就会从 bucket 中删除一个 binding
beginScope: pushes a special marker onto the stack | 将一个特殊的标记推入栈中
endScope: pops symbols off the stack until finds the topmost marker. | 弹出符号直到找到最顶部的标记
The auxiliary stack can be integrated into the Binder by having a global variable top showing the most recent Symbol bound in the table. | 可以将 auxiliary stack 集成到 Binder 中，通过一个全局变量 top 来显示最近绑定的符号
Pushing: copy top into the prevtop field of the Binder. | 将 top 复制到 prevtop 字段中

Binder

struct TAB_table_ { 
    binder table[TABSIZE]; 
    void *top;
};

static binder Binder(void *key, void *value, binder next, void *prevtop) {
    binder b = checked_malloc(sizeof(*b));
    b->key = key; 
    b->value = value; 
    b->next = next; 
    b->prevtop = prevtop;
    return b;
}

Type Checking👀

类型及其作用👀

编程语言中的类型

变量的类型：
- 限制了变量在程序执行期间的取值范围
类型化的语言 (typed language)：
- 变量都被给定类型的语言，如 C/C++、Java、Go
- 表达式、语句等程序构造的类型都可以静态确定
未类型化的语言 (untyped language)
- 不限制变量值范围的语言 (no static types, 而非没有类型), 如 LISP、JavaScript

类型在编程语言中的作用:

开发效率：更高层次的编程抽象, e.g.,
- 多态、代数数据类型、依赖类型…
- hoogle利用类型信息搜索API
运行性能：类型指导的编译优化, e.g.,
- 静态类型绑定避免运行时检查
- 类型信息优化内存布局
安全可靠：内存安全乃至功能正确, e.g.,
- Rust线性类型保障内存安全
- LiquidHaskell 精化类型保障功能正确

Tiger 类型系统👀

Type Checking 中的关键问题

What are valid type expressions ?
- 总共有哪些类型，每个类型表达式对应到什么?
- e.g., int, string, unit, nil, array of int, record …
How to define two types are equivalent ?
- 比如，两个 record 类型是否相同?
What are the typing rules ?
- 要检查什么，比如形参和实参是否一致?

1) 首先回顾 Tiger 语言总共有哪些类型：

基本类型：int, string
复合类型：record, array | using records and arrays from other types (primitive, record, or array)

类型的文法定义和声明案例

那么如何将 type identifier 和 expression 绑定起来？

当处理相互递归类型时：Ty_Namw(sym, NULL)
- a place-holder for the type-name sym

2) 类型等价 (Type Equivalence)：

有如下两种等价关系：

Name equivalence (NE): T1 and T2 are equivalent iff T1 and T2 are identical type names defined by the exact same type declaration.
Structure equivalence (SE): T1 and T2 are equivalent iff T1 and T2 are composed of the same constructors applied in the same order.

type a = {x:int, y:int}
type ptr = {x:int, y:int}
function f(a : point) = a

Tiger 使用 Name Equivalence，E.g., point and ptr are equivalent under SE but not equivalent under NE

Type equivalence 影响类型检查，如是否需要在 Typing environment 增加新的类型? 函数的形参和实参类型识别匹配?

类型等价

要注意每一个 record type expression 都创建一个新的、不同的 record type

Example

IllegalLegal

let type a = {x:int, y:int}
    type b = {x:int, y:int}
    var i : a := ...
    var j : b := ...
in i := j
end

let type a = {x:int, y:int}
    type b = a
    var i : a := ...
    var j : b := ...
in i := j
end

3) Tiger 的命名空间

Tiger 有两个独立的命名空间：

Types
Variables and functions

TypeVariable and Function

let type a = int
    var a := 1
in ...
end

Both a can be used.

let function a(b : int) = ...
    var a := 1
in ...
end

variables and functions of the same name cannot both be in scope simultaneously (one will hide the other) | 变量和函数不能同时存在，一个会隐藏另一个
var a hides function a

Tiger 类型检查👀

Tiger 语义分析需要维护 2 个环境:

Types environment: Maps type symbol to type that it stands for Symbol -> Ty_ty
Variables and functions environment:
- Maps variable symbol to its type.
  - E.g., Symbol -> Ty_ty
- Maps function symbol to parameter and result types.
  - E.g., Symbol -> struct {Ty_tyList formals; Ty_ty result}

预定义环境

codeExplanation

typedef struct E_envent_ *E_envent;
struct E_enventry_ {
    enum {E_varEntry, E_funEntry} kind; 
    union {
        struct {Ty_ty ty;} var;
        struct {Ty_tyList formals; Ty_ty result;} fun; 
        } u;
};
E_enventry E_VarEntry(Ty_ty ty); 
E_enventry E_FunEntry(Ty_tyList formals, Ty_ty result);

S_table E_base_tenv(void); /* Ty_ty environment */ 
S_table E_base_venv(void); /* E_enventry environment */

Predefined type and value environments

Type environment “int” $\mapsto$ Ty_Int(), “string” $\mapsto$ Ty_String()
Value environment contains predefined functions of Tiger

对于语义分析, 既做语义检查又做中间代码 (IR Code) 生成。同时对 expressions 和 declarations 进行检查

现在还不用考虑 IR code 生成

Implementation

The Semant module (semant.h, semant.c) performs semantic analysis including type-checking – of abstract syntax
Semantic analysis: four recursive functions over AST

Semantic analysis

Struct expty transVar (S_table venv, S_table tenv, A_var v); 
struct expty transExp (S_table venv, S_table tenv, A_exp a);
void transDec (S_table venv, S_table tenv, A_dec d);
Ty_ty transTy (S_table tenv, A_ty a);

Type-checking expressions
Type-checking declarations
- Variable declarations
- Type declarations
- Function declarations
- Recursive type declarations
- Recursive function declarations

Type-checking expressions👀

Struct expty transExp (S_table venv, S_table tenv, A_exp a);

transExp: Type-checking expressions: query && update the environments
Input:
- venv: value environment
- tenv: type environment
- a: expression to be type-checked
Output:
- a translated expression and its Tiger-language type

Rules:

Function call: the types of formal parameters must be equivalent to the types of actual arguments.
If-expression: if exp1 then exp2 else exp3
- The type of exp1 must be integer, the types of exp2 and exp3 should be equivalent.

此处举两个例子，其余见虎书附录

Type-checking declarations👀

Declarations 会修改 environments，且在 Tiger 语言中，declaration 只能出现在 let 中 (let 中的声明可以在 in 中使用)

1) Variable Declarations

Processing a variable declaration without a type constraint:

var x := exp

Processing a variable declaration with a type constraint:
- 需要检查 constraint 和 initializing expression 的类型是否一致
- 同时，initializing expressions of type Ty_Nil must be constrained by a Ty_Record type.

var x: type-id := exp

2) Type Declarations:

非递归类型声明，如 type type-id = ty

transTy 函数将 ty 递归转换为 Ty_ty 类型

Info

可以直接利用抽象语法树 (AST) 节点上的类型信息 (A_ty)

void transDec (S_table venv, S_table tenv, A_dec d) {
    ...
    case A_typeDec: {
        S_enter(tenv, d->u.type->name, transTy(tenv, d->u.type->ty));
    }
    ...
}

NOTICE: This program fragment only handles the type-declaration list of length 1!

3) Function Declarations:

非递归函数声明，如 function id (tyfields) ： type-id = exp

…

4) Recursive Type Declarations:

首先考虑如何将声明 type list = {first:int, res:list} 转化为 internal type representations？

困难在于：需要从 type environment 中找到 list 的定义，但是此时 list 还没有被定义。
解决办法是：use two passes
1. Put all the “headers” in the environment first (即便他们还没有 bodies)
  1. 例如上例中：type list = 就是一个 header
  2. Use the special “name” type for the header
2. Call transTy on the “body” of the type declaration
  1. 对于上例，record type expression {first:int, res:list} 就是 body
  2. The type that transTy returns can then be assigned into the ty field within the Ty_Name struct.

Tiger 语言的重要特性之一

Every cycle in a set of mutually recursive type declarations MUST pass through a record or array declaration！| 在一组相互递归的类型声明中，每个循环都必须经过记录或数组声明

Example

手动递归函数声明

手动处理递归函数也是类似.E.g., f call g, g call f
Problem: 在处理函数声明的右侧时，我们可能会遇到 env 中尚未定义的符号
Solution:
- First pass: gathers information about the header of each function but leaves the bodies of the functions untouched.
- Second pass: processes the bodies of all functions with the augmented environment.

Activation Record👀

较简单，可略看

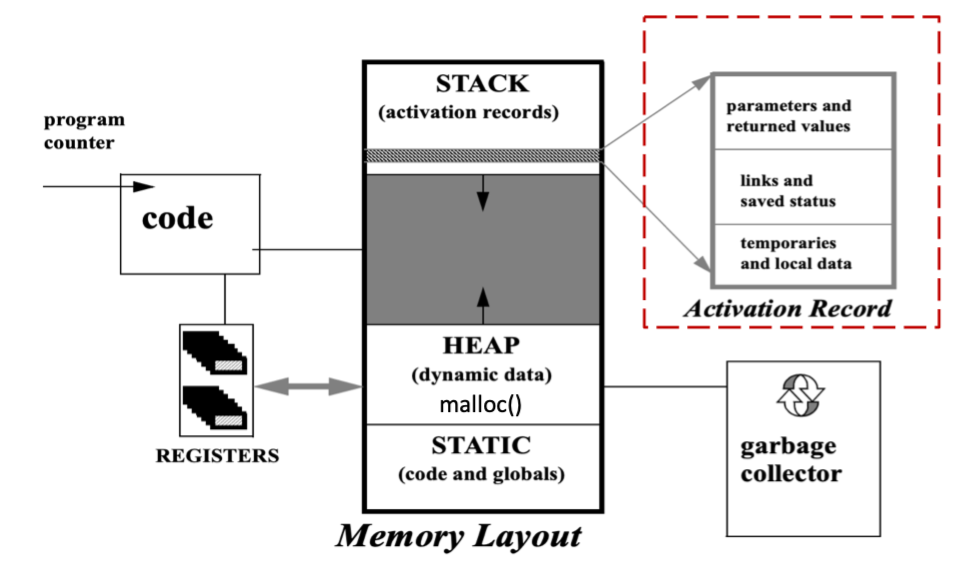
Overview of a Morden Processor

由四部分组成：

ALU 算术逻辑单元：执行算术和逻辑运算
Registers 寄存器：存储临时数据 (有限数量但速度快，且用途大多相同，少部分有特殊用途，如 PC, SP)
Control: 控制单元，执行指令，控制数据流向 (指令存储在内存中)
Memory: 存储数据和指令 (地址空间是程序使用内存的方式)

程序的运行时 内存布局 如下：

本节聚焦于 Activation Record，即活动记录

活动记录在函数 (Function)、过程 (Procedure) 和方法 (Method) 调用中起着重要作用，其实就是函数调用的栈帧

函数和 API、ABI 很相似：

API (Application Programming Interface): 源程序之间的接口
ABI (Application Binary Interface): 本节的主题就是如何实现 ABI
- 二进制程序之间的接口 (甚至可以是不同编译器编译编程语言的程序)
- Conventions on low-level details：
  - 如何传递参数？
  - 如何返回值？
  - 如何处理寄存器？
  - …

通常情况下，function 和 method 视为同一种东西。

tiger 将过程和函数区分开来，过程没有返回值，函数有返回值

Stack Frame👀

Function Invocation

An invocation of function P is an activation of P
那么如何保存局部变量？

Each invocation has its own instantiation of local variables | 每次调用都有自己的局部变量实例化
函数调用遵循后进先出（LIFO）原则
使用 LIFO 数据结构 —— 一个栈

Activation record Or stack frame (栈帧): a piece of memory on the stack for a function
栈帧连接了 caller 和 callee, E.g.,
- Relevant machine state (saved registers, return address) | 相关机器状态
- Space for return value | 返回值空间
- Space for local data | 本地数据空间
- Pointer to activation for accessing non-local data | 访问非本地数据的激活指针

由此引入 关键问题：如何布局 Activation record，以便调用者和被调用者能够正常通信？

活动记录的设计👀

《深入理解计算机系统》中的 Stack Frame 例子

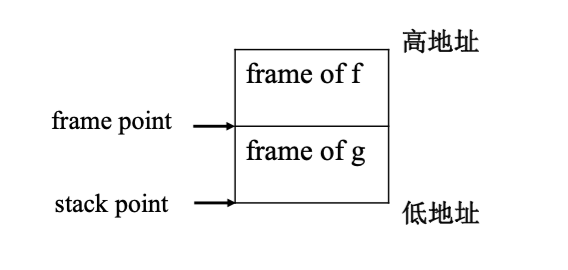
Stack Frame 从高地址往低地址增长

对于 Frame 和 Stack 指针：

Frame Pointer (FP) (base pointer, 基址寄存器)
- 指向当前帧的起始位置
- 编编译代码引用局部变量和参数的方式是使用帧指针的偏移量
- E.g., x86: ebp, rbp; ARM: fp
Stack Pointer (SP) (top of stack, 栈顶指针)
- 指向当前帧的栈顶 (最低地址)
- Referring to the top of the stack
- E.g., x86: esp, rsp; ARM: sp

Workflow Of Function Call

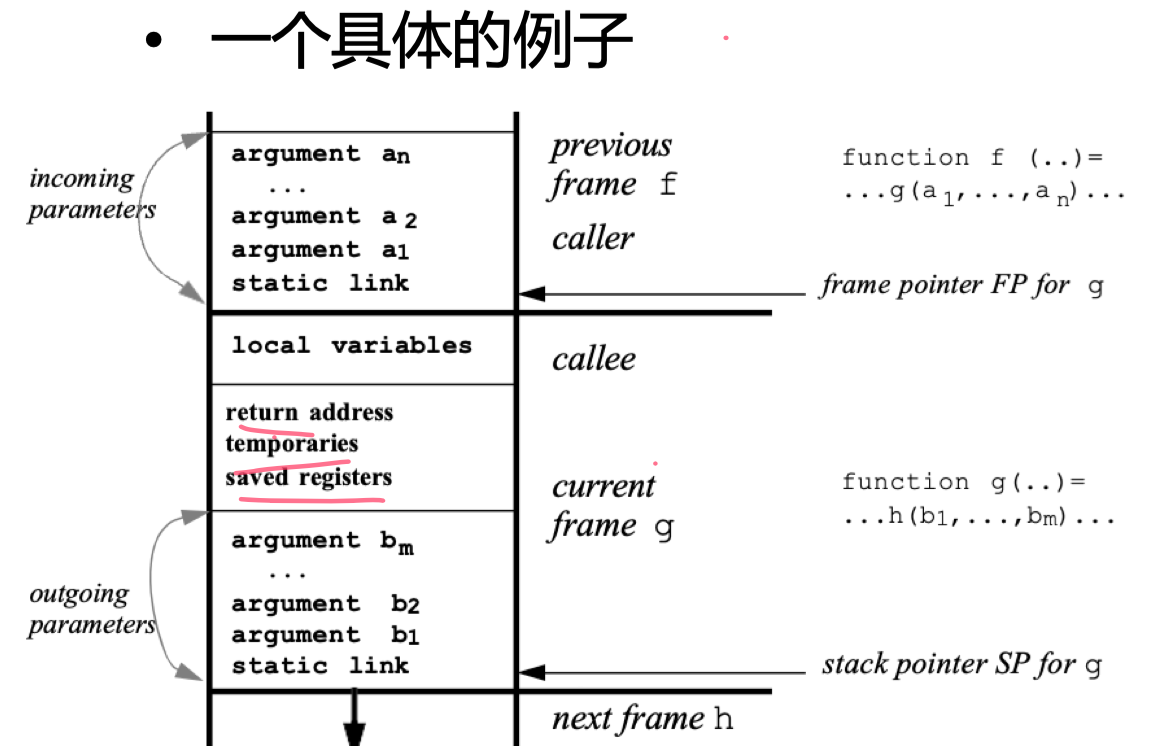
f(…) 函数调用 g(a1, …, an) 函数的过程：

当 f 调用 g 时:
- 堆栈指针指向f传递给g的第一个参数
- g 通过简单地从堆栈指针（SP）减去帧大小来分配一个帧
当进入 g 时：
- 将旧的帧指针FP保存在帧中的内存中
- FP = SP
当从 g 返回时：
- SP = FP
- 恢复保存的旧帧指针 (FP)

Use of Registers👀

How to reduce memory traffic?

Recap: Memory Hierarchy

访问寄存器比访问内存快得多

Problem: Putting everything in the stack frame can cause the memory traffic
Solution: Hold as much of the frame as possible in registers
- (Some) function parameters
- Function return address
- Function return value
- (Some) Local variables
- (Some) Intermediate results of expressions (temporaries)

Using Registers: 参数传递👀

Tiger 的参数方式：Call-by-Value

实际参数的值被传递并作为形式参数的值确立。

对形式参数的修改不会影响实际参数。

Problem: passing parameter stack causes memory traffic

Solution (现代机器的参数传递约定)：

The first k arguments ( k = 4 or 6) are passed in registers
The rest are passed on the stack

虽然通过将部分参数传递到寄存器中可以减少内存流量，但是这种方法也有一些问题 : extra memory traffic caused by passing arguments in registers!

Solution: “Saving” the status of registers

More about Register Saving Conventions

考虑一种场景:

f(int a) {
    int z = ...
    h(z);
    ...
    int t = a + 1;
    ...
}

假如 f 从寄存器 r1 中得到参数 a，随后通过寄存器 r1 将 z 传递给 h
那么 f 在调用 h 之前需要保存 r1 的状态，以便在调用 h 之后恢复

如何避免 extra memory traffic 呢？

如果在 f 中调用 h 之前，a 已经是一个 dead variable，那么就不需要保存 r1 的状态 (比如，不存在第五行，那么就需要对代码预先做分析)
也可以使用 global register allocation: 不同的函数使用不同的寄存器组，这样就不需要保存寄存器状态 (例如，r1 可以用于 f，r2 可以用于 h)
Leaf procedures (没有调用其他函数的函数) 可以不保存寄存器状态
使用 register windows (SPARC)：每个函数调用可以申请一组新的寄存器，这样就不需要保存寄存器状态

Using Registers: Others👀

1) 对于返回地址：

在现代机器上，调用指令只是将返回地址放到指定的寄存器中；
nonleaf procedures 必须将其写入堆栈（除非使用了 interprocedural register）, 叶子过程则不需要

2) 对于返回值：

通常情况下，返回值被 callee 放在指定的寄存器中

3) 对于 Locals and Tempories:

一些局部变量和临时变量（如表达式的中间结果）可以放在寄存器中，以减少内存流量

在寄存器分配一节中详细讨论关于局部变量和临时变量的问题

Frame-Resident Variables👀

A variable will be allocated in stack frames because:

It is passed by reference，因此他必须要有一个内存地址
Its address is taken, 例如，通过 & 操作符
It is accessed by a procedure nested inside the current one; | 它通过当前程序中嵌套的程序来访问；
这个值太大，无法放入单个寄存器中；
该变量是一个数组，需要进行地址运算来提取组件；
保存变量的寄存器有特定用途，比如传递参数（如上所述）；
局部变量和临时变量太多，导致“溢出” （将在讨论寄存器分配时详述）

逃逸情况

The variable escapes¹ for any of the reasons:

通过引用传递，因此它必须有一个内存地址；
它的地址被获取，例如，在C语言中是 &a；
它被当前函数内部的嵌套过程访问。

Example

pass-by-reference (在 Pascal 中支持，但 Tiger 不支持)：

真实的变量位置传递；
对形式参数的引用隐含着访问实际参数值的间接访问。
对形式参数的修改确实会改变实际参数！

Block Structure👀

Tiger 语言嵌套函数的实现

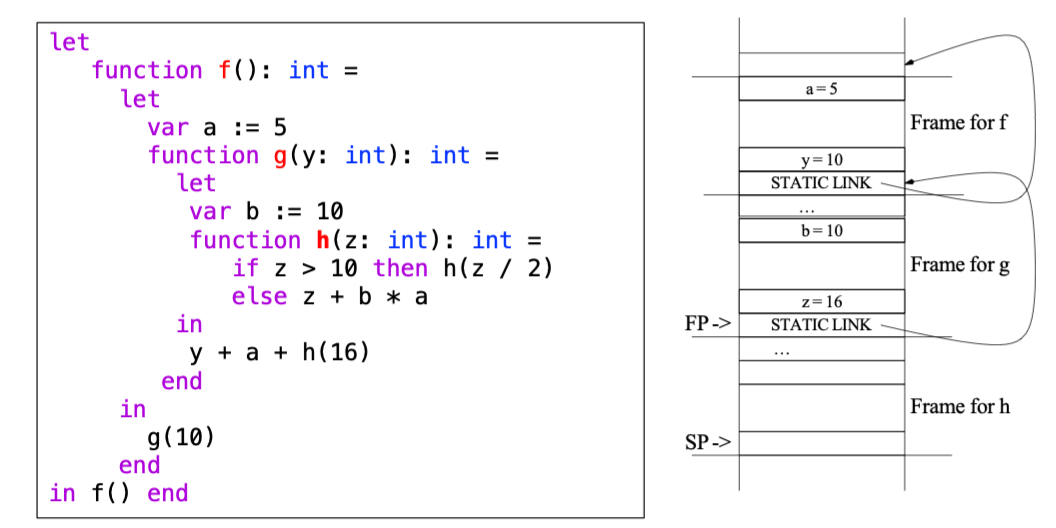
Static Link (重点)👀

使用 static link 的动机源自于 block structure 的实现

Abstract

Whenever a function g is called, it can be passed a pointer to the frame of the function statically enclosing g; this pointer is the static link. | 每当函数 g 被调用时，可以传入一个指向静态包围 g 的函数帧的指针；这个指针就是静态链接。

考虑上图，Static Link -> 每当函数 g 被调用时，它会接收到一个指针，该指针指向程序文本中立即包围 g 的 f 函数的最新活动记录｜Whenever g is called, it is passed pointer to most recent activation record of f that immediately encloses g in program text

The static link is a pointer to the activation record of the enclosing procedure

可以使用 static link 访问 non-local data:

每个函数标有其嵌套深度
当深度为 n 的函数访问深度为 m 的变量时，生成代码以向上爬 n-m 层 link，以访问合适的活动记录

Example

Cstatic link

int f (int x, int y)
{
    int m;
    int g (int z)
    {
        int h ()
        {
            return m + z;
        }
        return 1;
    }
    return 0;
}

int f(link, int x, int y)
{
    int m;
    int g(link, int z)
    {
        int h(link)
        {
            return link->prev->m + link->z;
        }
        return 1;
    }
    return 0;
}

优缺点

优点：
- Little extra overhead on parameter passing
缺点：(主要是 climb up link 的开销)
- 需要为每个变量访问建立一系列间接内存引用
- 间接引用的数量等于变量声明函数和使用函数之间的嵌套深度差
- 函数可能深嵌套！

Lambda Lifting👀

Abstract

When f calls g, each variable of f that is actually accessed by g (or by any function nested inside g) is passed to g as an extra argument. This is called lambda lifting. | 当函数f调用函数 g 时，f 中被 g（或 g 内部嵌套的任何函数）实际访问到的每个变量，都会作为额外的参数传递给 g。这被称为 Lambda Lifting。

当函数 g 调用 f 时，f（或 f 内部嵌套的任何函数）实际访问的 g 中的每个变量都会作为额外参数传递给 f。
- 通过将非局部变量视为形式参数来重写程序
转换过程从最内层的程序开始，逐渐向外层推进。

Example

具体实现应该是传地址

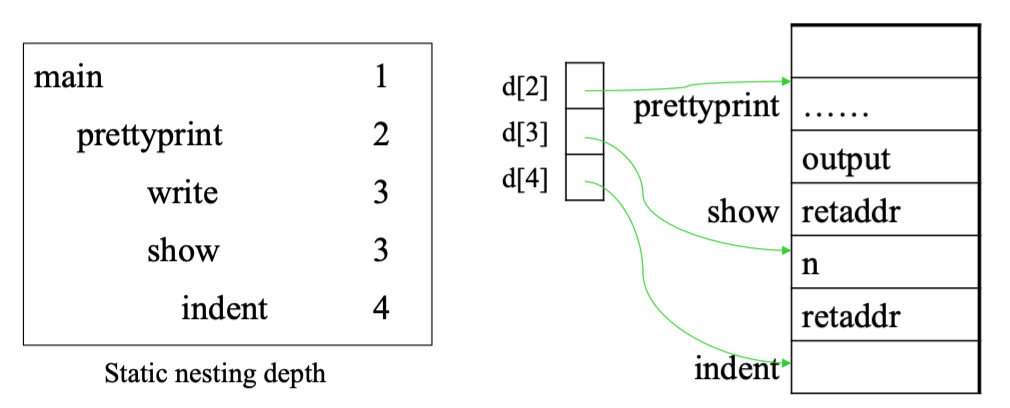
Display👀

Abstract

A global array can be maintained, containing – in position i – a pointer to the frame of the most recently entered procedure whose static nesting depth is i. This array is called a display | 可以维护一个全局数组，其中在位置i存储最近进入的、静态嵌套深度为 i 的程序的帧指针。这个数组被称为显示体。

Display: a global array of pointers to frames

它记录了程序的词法嵌套结构
在位置i —> 指向最近进入的、静态嵌套深度为 i 的 procedure 的帧的指针
本质上，它指向当前设置的包含可访问变量的活动记录集合

Example

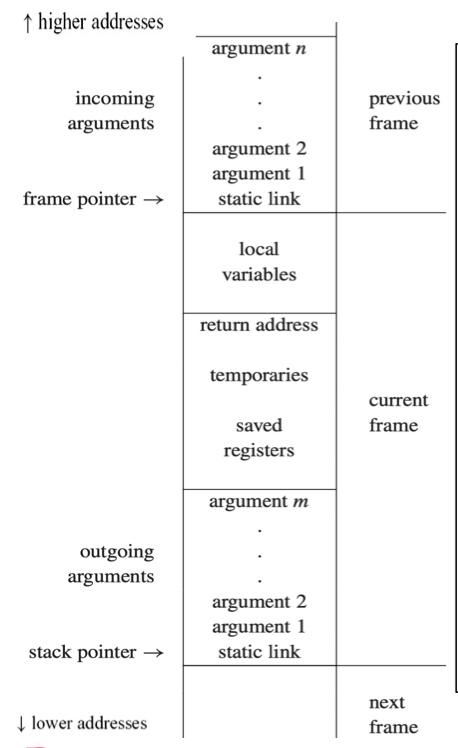
Stack Frame in Tiger👀

和之前提到的 Stack frame 可能有所不同，考试以这一部分为主

A Typical Stack Frame Layout for Tiger

incoming arguments: passed by the caller
return address: where (within the calling function) control should return:
- created by the CALL instruction
some local variables are in this frame, other local variables are kept in registers
saved registers: make room for other uses of the registers
outgoing argument: pass parameters to other functions
static link
Frame point 为特定寄存器 (如rbp, SP)，其值为栈上的内存地址
- 该地址的内存中所保存值是 stack link (某个函数的 frame point)

关于 incoming & outgoing arguments 的例子

On each procedure call or variable access, a chain of zero or more fetches is required; the length of the chain is just the difference in static nesting depth between the two functions involved. | 在每次函数调用或变量访问时，可能需要零个或多个取值操作；这个操作链的长度正是涉及的两个函数之间静态嵌套深度的差值。

Important

Static links may skip dynamic frames between f and g. They always point to the most recent frame of the routine that statically encloses the current routine. | 静态链接可能会跳过介于 f 和 g 之间的动态帧。它们始终指向当前程序被静态包含的最新帧。

Limitation of Stack Frame

Hard to support higher-order function: 支持高阶函数较为困难, 涉及嵌套函数与函数作为参数及返回值的组合。
在支持高阶函数的语言中，函数返回后可能需要保留局部变量。
但到目前为止，我们假定函数 f 返回后局部变量不会被使用（所以我们使用栈来存储）

	Pascal; Tiger	C	ML; LISP; Haskell
Nested functions	Yes	No	Yes
Procedure passed as arguments and results	No	Yes	Yes

关于 Tiger 编译器中 Frame 的补充👀

TODO

通俗来讲，当一个对象的指针被多个方法或线程引用时，则称这个指针发生了逃逸。逃逸分析决定一个变量是分配在堆上还是分配在栈上。 ↩

本文总阅读量: 次