Parsing (Top-Down Parsing)👀

约 5896 个字 60 行代码预计阅读时间 20 分钟

Abstract

本节主要介绍语法分析 (Parsing) 和上下文无关文法 (Context-Free Grammar, CFG) 的基本概念
和自顶向下的语法分析方法

上下文无关文法 | Context-Free Grammar👀

Note

CFG 是一种形式文法，用于描述上下文无关语言 (Context-Free Language) 的语法结构.

CFG 简介👀

问题: 如何形式化定义编程语言的语法？

语法分析的目的是教会计算机判断输入合法性

例：简单计算器程序

1 + 2 - 3 +     非法
1 + 2 - a       非法
1 + (2 - 3)     合法
1 2 + - 3       非法

如何判定输入合法性 & 生成语法树

首先规定好合法的基本单元 (Token) —— 词法分析
其次要理解算术表达式的构成
- 大表达式可拆分为子表达式
- 拆解过程是递归的，直至看到基本单元

如何构造编程语言的语法分析器

用 CFG 定义一个编程语言的语法
基于 CFG 构建解析器:
- Top-Down Parsing | 自顶向下的语法分析
- Bottom-Up Parsing | 自底向上的语法分析
More about parsing:
- Automatic paraser generation
- Error recovery

CFG 的定义👀

上下文无关文法: 描述语言的语法结构

\[G = (T, N, P, S)\]

$T$: 终结符集合 (Terminals), 组成串的基本符号 (Token)
- 例：$T = \{\text{num}, +, -, (, )\}$
$N$: 非终结符集合 (Non-terminals), 表示串的集合的语法变量 (在程序语言中通常对应于某个程序构造)
- 例：$N = \{\text{expr}, \text{term}, \text{stmt}\}$
$P$: 产生式集合 (Productions), $A \rightarrow a$, $A \in N$, $a \in (T \cup N)^*$
- 头(左)部 $A$ 是一个非终结符，右部 $a$ 是一个符号串
- 描述了一个将终结符和非终结符组合成串的方法
- e.g. $E \rightarrow E + E$, $E \rightarrow (E)$, $E \rightarrow \text{id}$
$S$: 开始符号 (Start symbol), $S \in N$
- 某个被指定的非终结符号
- 它对应的串的集合就是文法的语言

$T \cap N = \emptyset$

$T \cup N$ : 文法符号集

EOF Marker

$: end of file (EOF)
To indicate that $ must come after a complete $S$ -phrase
- add a new start symbol $S'$ and a new production $S' \rightarrow S\$$

产生式的缩写👀

对一组有相同左部的 $\alpha$ 产生式

\[\alpha \rightarrow \beta_1, \dots, \alpha \rightarrow \beta_n\]

可以简记为：

\[\alpha \rightarrow \beta_1 \vert \dots \vert \beta_n\]

读作：$\alpha$ 定义为 $\beta_1$ 或 $\dots$ 或 $\beta_n$
$\beta_1, \dots, \beta_n$ 称为 $\alpha$ 的候选式 (Candidate)

推导和归约👀

问题：给定文法，如何判定输入串属于文法规定的语言?

推导 (Derivations) 和归约 (Reductions)

\[\text{给定文法}~ G=(T, N, P, S)\]

直接推导：把产生式看成重写规则，把符号串中的非终结符用其产生式右部的串来代替
- 如果 $A \rightarrow \gamma \in P$, 且 $\alpha, \beta \in (T \cup N)^*$, 称串 $\alpha A \beta$ 直接推导出 $\alpha \gamma \beta$, 并记作 $\alpha A \beta \Rightarrow \alpha \gamma \beta$
直接归约：如果 $\alpha A \beta \Rightarrow \alpha \gamma \beta$, 则称 $\alpha \gamma \beta$ 直接归约到 $\alpha A \beta$
多步推导：如果 $\alpha_0 \Rightarrow \alpha_1$, $\alpha_1 \Rightarrow \alpha_2$, $\dots$, $\alpha_{n-1} \Rightarrow \alpha_n$, 则可以记作 $\alpha_0 \Rightarrow \alpha_1 \Rightarrow \dots \Rightarrow \alpha_n$, 称符号串 $\alpha_0$ 经过 n 步推导得到 $\alpha_n$，可简记为 $\alpha_0 \Rightarrow^n \alpha_n$
- $\Rightarrow^+$ 表示“经过正数步推导”
- $\Rightarrow^*$ 表示“经过零步或多步推导”

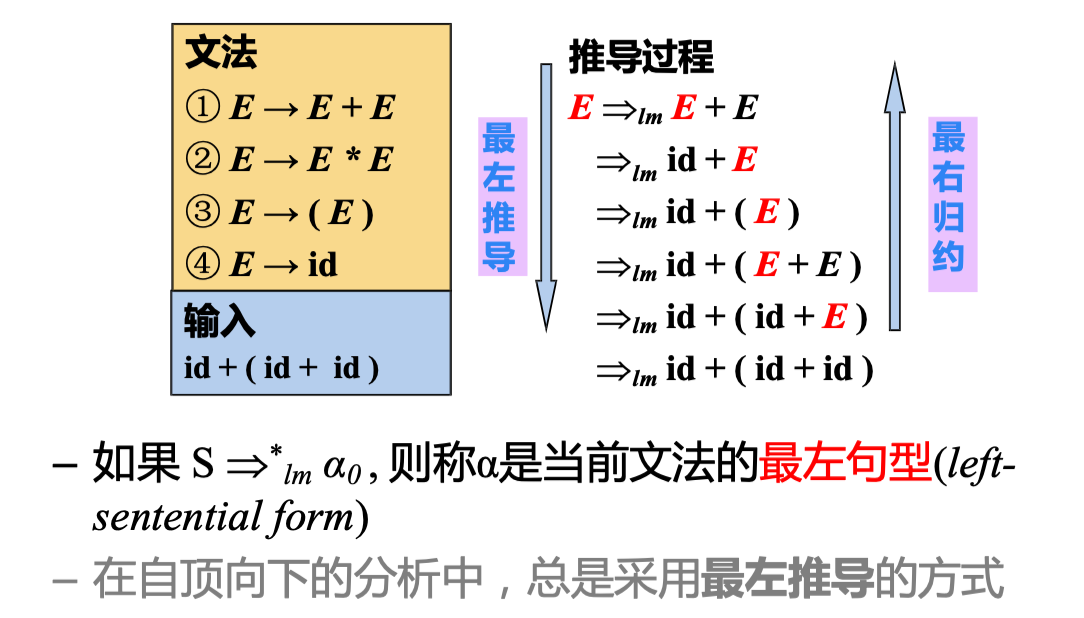
1) 最左推导 (Left-most Derivation)：每步代换 最左边的非终结符

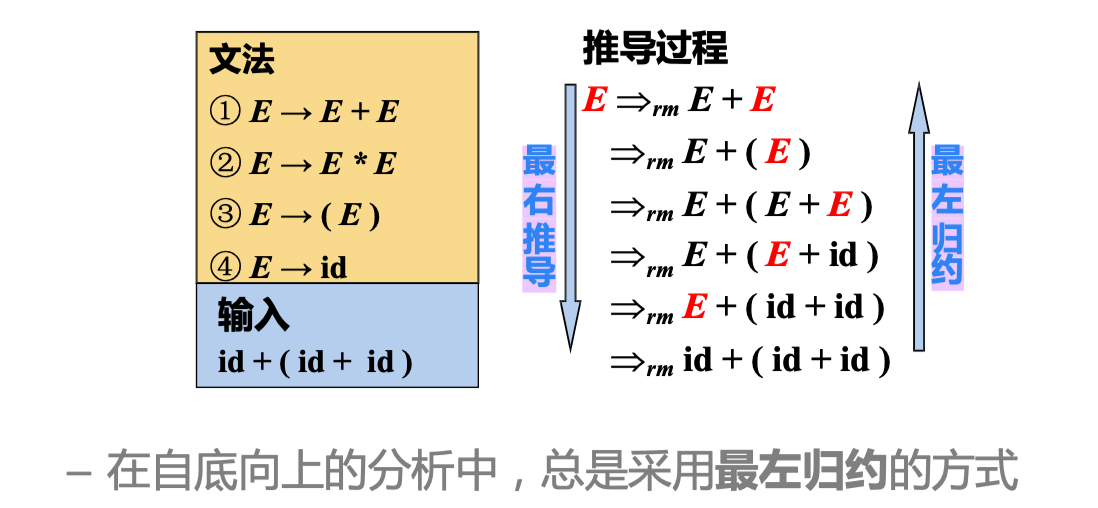
2) 最右推导 (Right-most Derivation)：每步代换 最右边的非终结符

3) 句型、句子和语言

句型 (Sentence Form)：对开始符号为 $S$ 的文法 $G$, 如果 $S \Rightarrow^* \alpha$, $\alpha \infty (T \cup N)^*$, 则称 $\alpha$ 为 $G$ 的一个句型
- 句型中既可以包含终结符，又可以包含非终结符，也能是空串
句子 (Sentence)：如果 $S \Rightarrow^* w$, $w \in T^*$, 则称 $w$ 为 $G$ 的一个句子
- 句子是不含非终结符的句型
语言 (Language)：由文法 $G$ 推导出的所有句子构成的集合，记为 $L(G)$

\[L(G) = \{w \vert S \Rightarrow^* w, w \in T^*\}\]

例: 文法定义的句型和句子

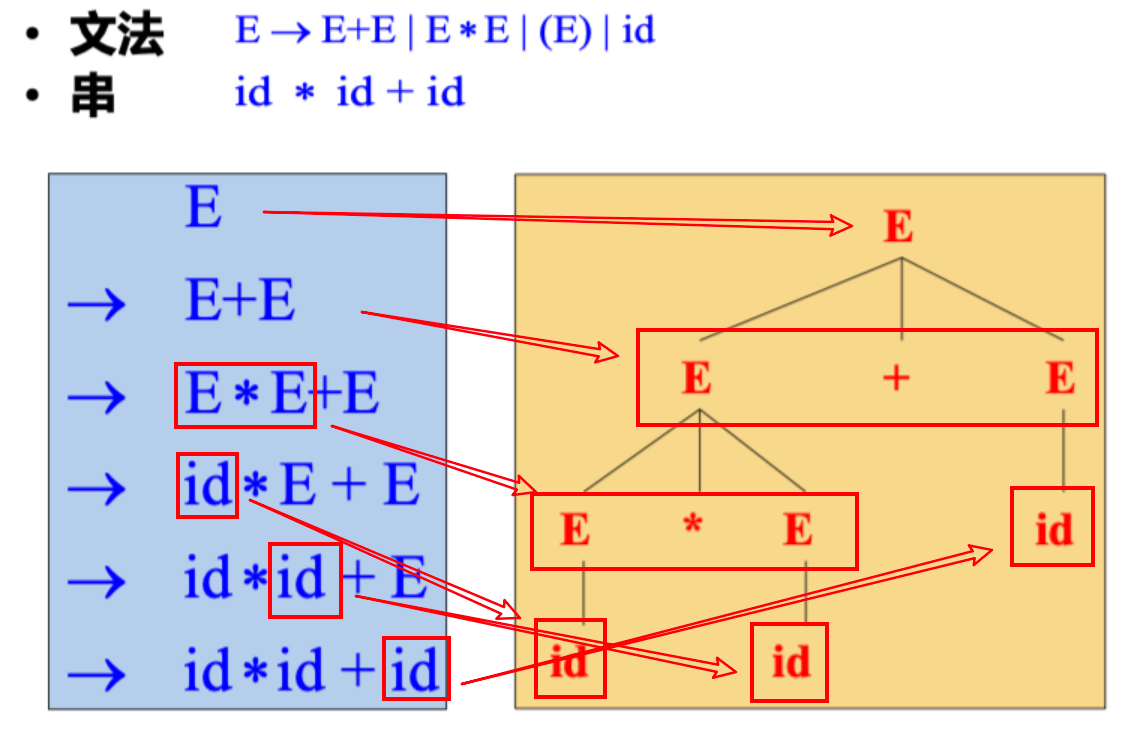
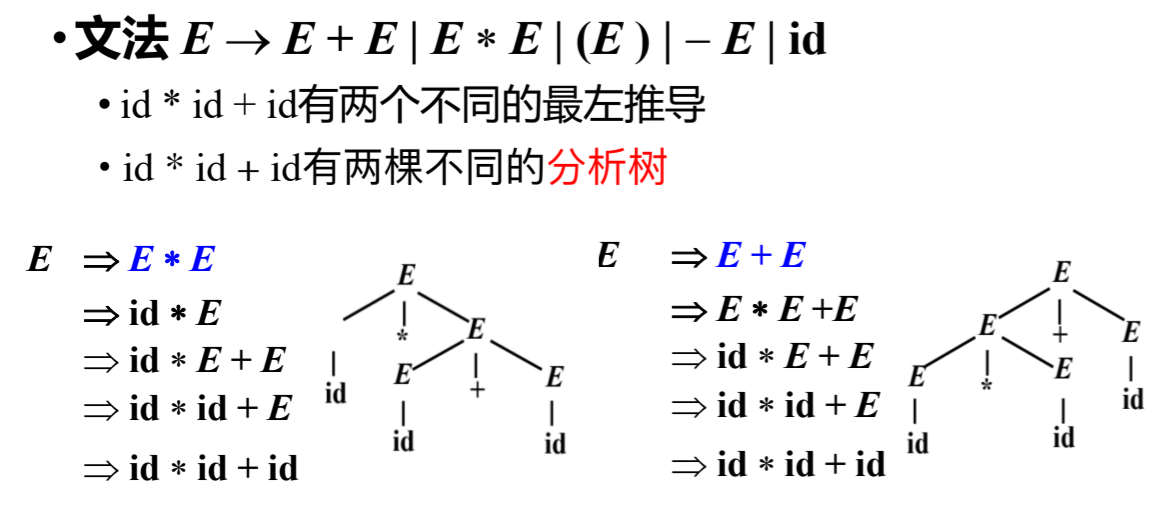
考虑文法：$E \rightarrow E + E \vert E * E \vert (E) \vert \text{id}$
存在一下推导序列：

\[E \Rightarrow -E \Rightarrow -(E) \Rightarrow -(E + E) \Rightarrow -(\text{id} + E) \Rightarrow -(\text{id} + \text{id})\]

$-(\text{id} + \text{id})$ 是文法的句子
$-(\text{id} + E)$ 是文法的句型

4) 输入串的判定

问题：给定文法，如何判定输入串属于文法规定的语言?

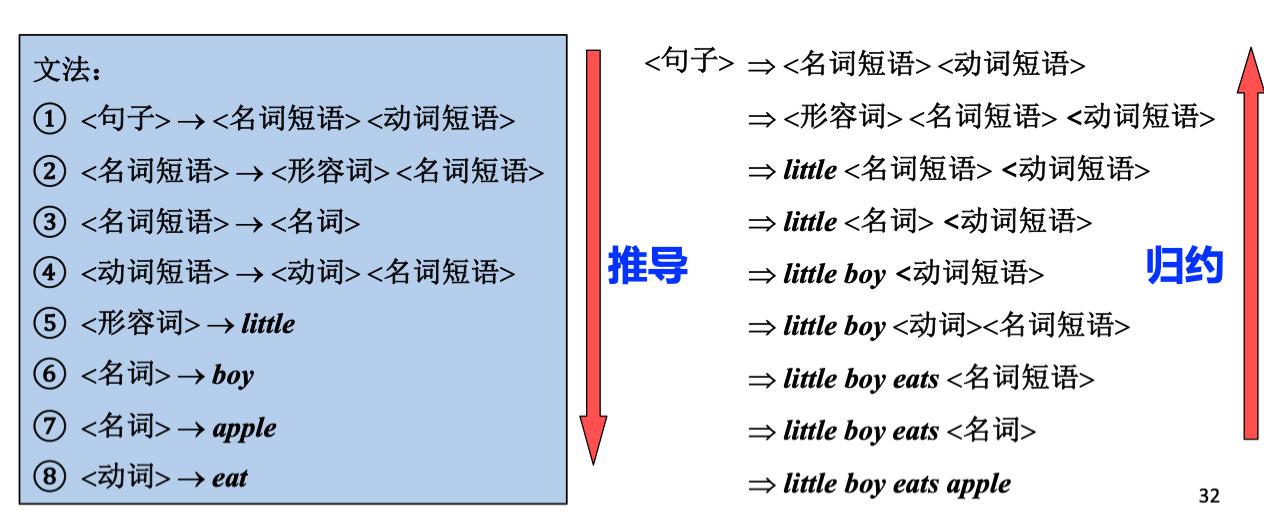
根据文法规则

从生成语言的角度 (句子的推导 (派生)) 出发，，从开始符号可以推导出该词串
从识别语言的角度 (句子的归约) 出发，从词串可以归约出开始符号

Example

RE 与 CFG👀

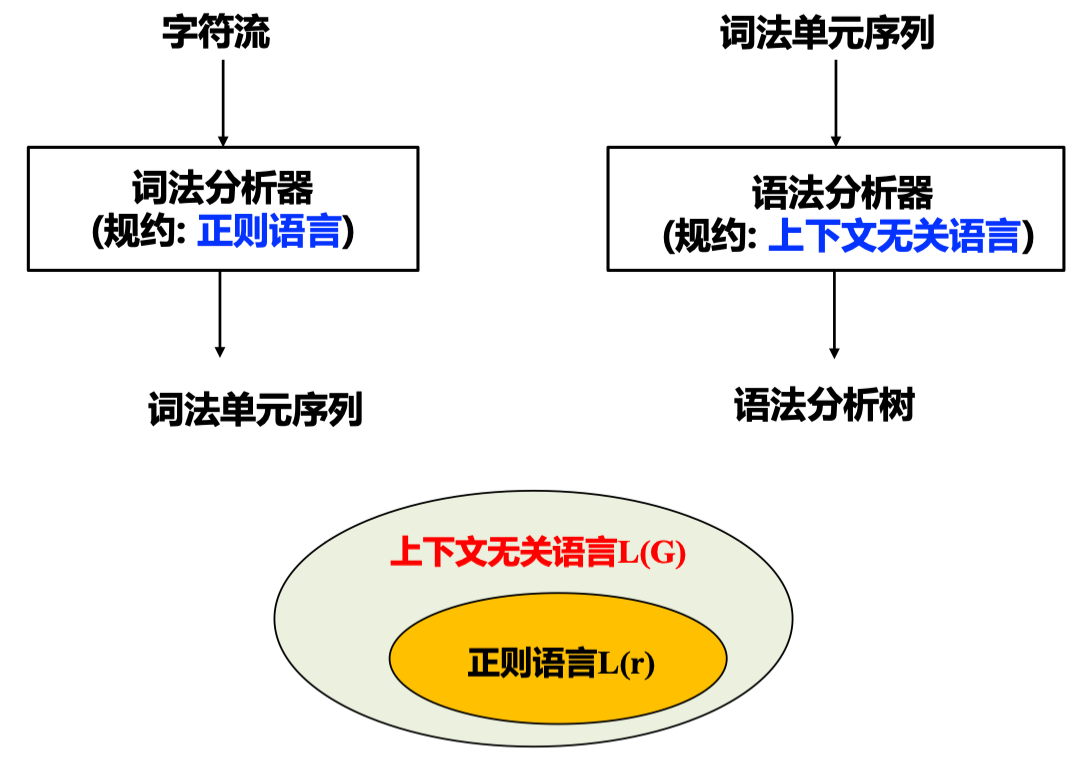
问题：为什么词法和语法分析用不同形式语言?

比较语法分析和词法分析

回顾形式语言, 正则语言(由正则表达式刻画), 上下文无关语言

正则文法 (正则语言的形式文法刻画) 的定义:

\[G = (N, T, P, S)\]

$N$: 非终结符集合
$T$: 终结符集合
$P$: 产生式 (Production) $\alpha \rightarrow \beta$ 集合
- 右线性文法：$\alpha \rightarrow \beta$ 形如 $A \rightarrow \alpha B$ 或 $A \rightarrow \alpha$，其中 $A, B \in N$, $\alpha \in T \cup \epsilon$
- 左线性文法：$\alpha \rightarrow \beta$ 形如 $A \rightarrow B \alpha$ 或 $A \rightarrow \alpha$
$S$: 开始符号, $S \in N$

正则语言：右线性文法/左线性文法产生的所有句子的集合

故从文法角度考虑，正则语言和上下无关语言对 $\alpha \rightarrow \beta$ 形式的限制不同：
- 上下无关文法：$\alpha$ 是一个非终结符号，右部是一个符号串
- 正则文法：右线性 $A \rightarrow \alpha B$ 或 $A \rightarrow \alpha$，左线性 $A \rightarrow B \alpha$ 或 $A \rightarrow \alpha$
- 上下文无关语言涵盖了正则语言，即每个正则语言都是一个上下文无关语言，反之不成立
从实用角度, 正则语言表达能力有限，难以刻画编程语言的语法
- 如: 不能用于描述配对或嵌套的结构
  - 例：配对括号串的集合，如不能表达 $(^n)^n, ~n\ge 1$
  - 原因：有穷自动机无法记录访问同一状态的次数

为什么词法分析用正则表达式，不用正则文法？

分离词法分析和语法分析

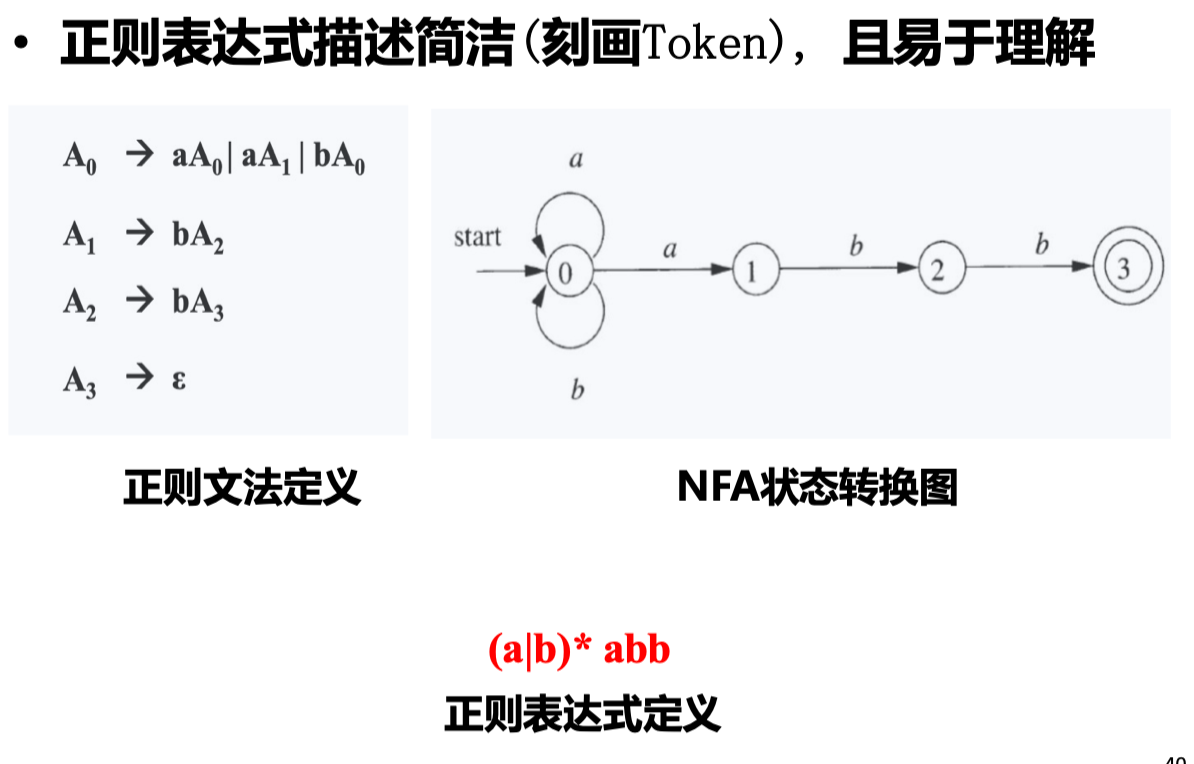
为什么用正则语言定义词法
- 词法规则非常简单，不必用上下文无关文法
- 对于 Token，正则表达式描述简洁且易于理解– 从正则表达式构造出的词法分析器效率高
分离词法分析和语法分析的好处
- 简化设计、提升性能
- 编译器的可移植性加强
- 便于编译器前端的模块划分

引申: 形式文法的分类

形式语言的文法分为 4 类：

\[\text{文法} ~ G = (T, N, P, S)\]

0 型文法 (短语结构文法): 递归可枚举语言
- $\alpha \rightarrow \beta$, $\alpha, \beta \in (T \cup N)^*$, $\vert \alpha \vert \ge 1$
1 型文法 (上下文有关文法)
- $\vert \alpha \vert \le \vert \beta \vert$, 但 $S \rightarrow \epsilon$ 可以例外
2 型文法 (上下文无关文法)
- $A \rightarrow B$, $A \in N$, $B \in (T \cup N)^*$
3 型文法 (正则文法)

引申: CFG 只能表达“语法”吗？

语法分析概述 | Parsing👀

CFG 的 Parse Tree👀

先不考虑抽象语法树 (Abstract Syntax Tree)

回顾推导和归约中输入串的判定

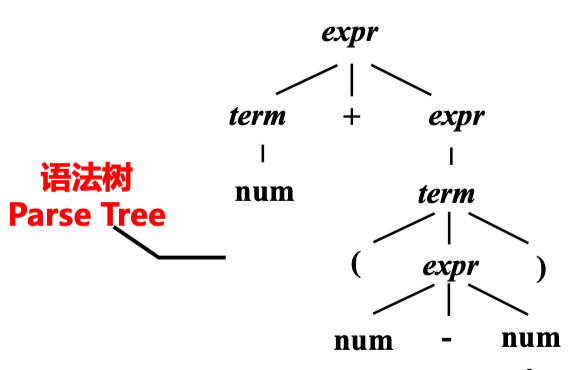
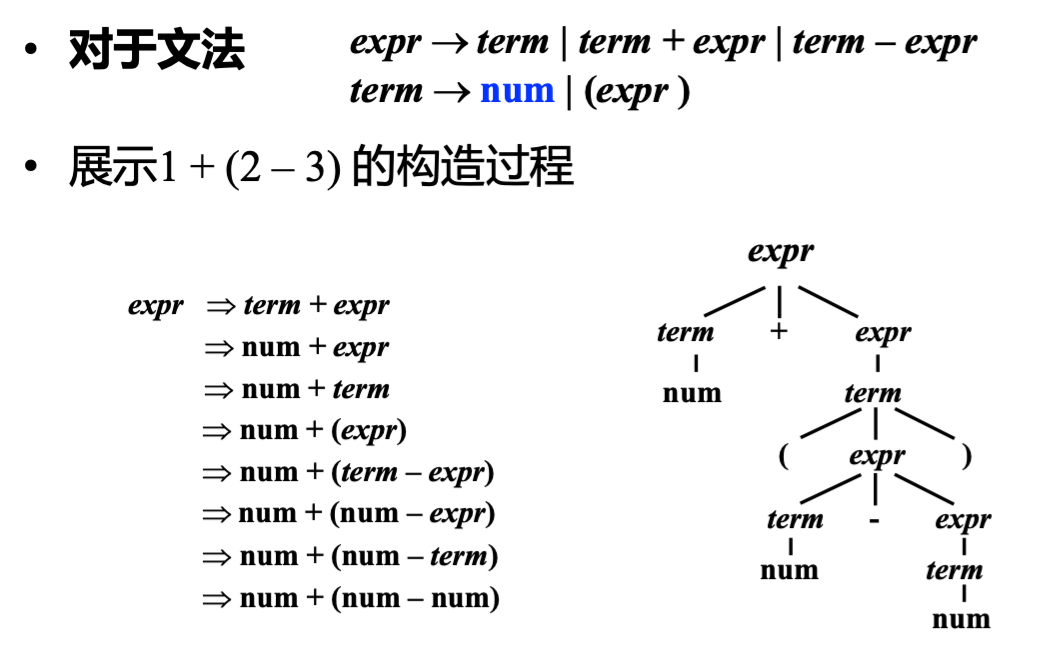
分析树 (Parse Tree) 可以看作是推导的图形化表示，其具有下面的性质：

根节点为文法的初始符号
每个叶子节点是一个终结符
每个内部节点是一个非终结符
每一个父节点和他的子节点构成一条产生式

可以将语法分析看作搜索问题，语法分析的核心问题就是：对于一个终结符号串 $x$, 设法从 $S$ 推导出 $x$ 或者从 $x$ 归约出 $S$

自顶向下 (Top-down) 分析
- 从开始符号 $S$ 出发，尝试根据产生式规则推导 (derive) 出 $x$
- Parse Tree 的构造方法：从根部开始
自底向上(Bottom-up) 分析
- 尝试根据产生式规则归约 (reduce) 到文法的开始符号 $S$
- Parse Tree 的构造方法: 从叶子开始

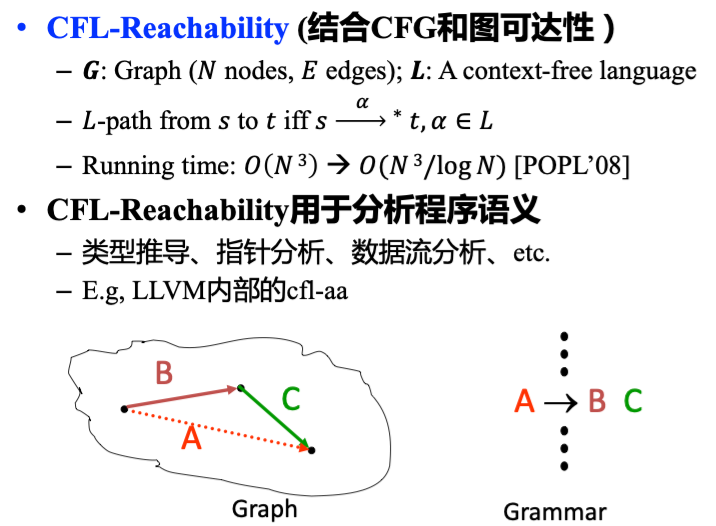
If there are no restrictions on the form of grammar used, parsing CFL requires $O(n^3)$ time

Subsets of CFLs typically require $O(n)$ time

Predictive parsing using $LL(1)$ grammars

Shift-Reduce parsing using $LR(1)$ grammars

设计编程语言的文法👀

为了高效语法分析，可能对文法做处理/限制

消除二义性 (Resolving Ambiguities)
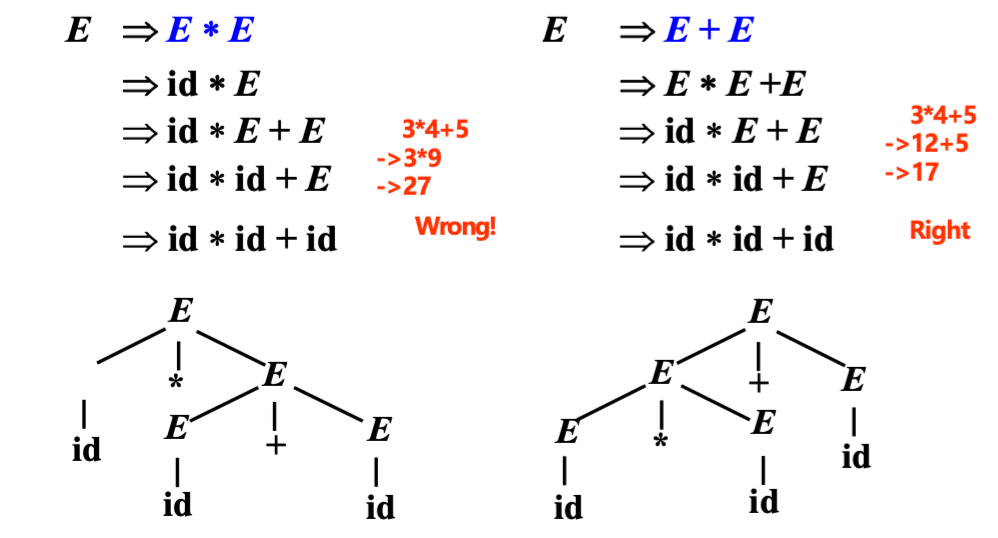
- 二义性：可以为一个句子生成多棵不同的分析树
消除左递归 (Elimination of left recursions)
- Avoid infinite loop in top-down parsing
提左公因子 (Left-factoring)
- Avoid backtracking in top-down parsing

其中，“消除左递归” 和 “提左公因子” 常限于自顶向下分析

二义性文法 (Ambiguous Grammar)👀

如果文法的某些句子存在不止一棵分析树，则该文法是二义的
“给定 CFG 是否无二义性?” 是不可判定问题¹
但能给出一组充分条件，满足这组充分条件的文法是无二义性的
- 满足，肯定无二义性
- 不满足，也未必就是有二义性的

Example

二义性的影响

编程语言的语法应该是无二义的。否则会导致一个程序有多种解释，如：

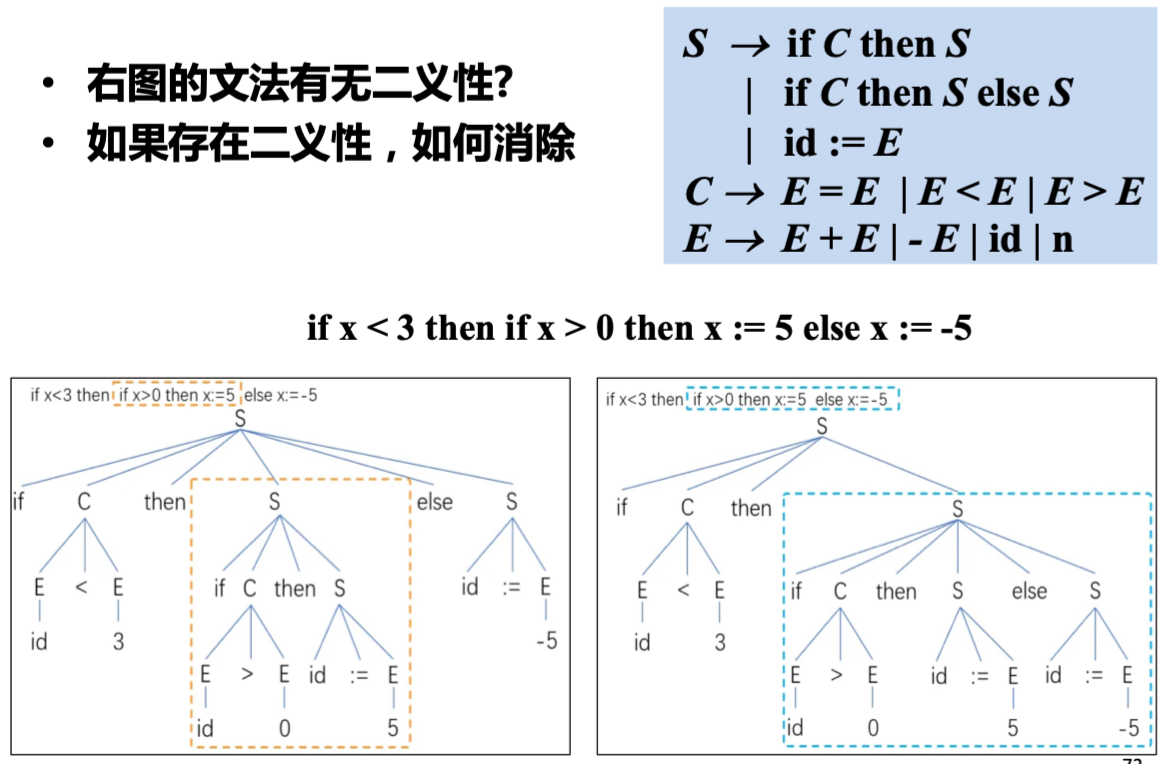
消除二义性👀

二义性的根源：多种 “正确” 推导处于文法同一层
消除二义性的惯用技术: 分层
- 改造文法，对于引发二义性的多种推导处于文法同一层的情况，将真正想要的推导提取出来，放到更深的层次
- 最左推导中，更深层的非终结符总是会被优先替换
- 确保只有一种最左推导，消除二义性

如：

E   -> E + E
    |  E * E
    |  (E)
    |  id

+ 和 * 操作都是左结合的，并且在运算中有不同的优先级，但是在这个文法中没有得到体现

所以消除二义性需要：

规定符号的优先级
规定符号的结合性

初始修改后

E   -> E + E
    |  E * E
    |  (E)
    |  id

E   -> E + T | T
T   -> T * F | F
F   -> (E) | id

+, * 都是左结合的，且 * 的优先级高于 +

运算优先级
- 根据算符不同的优先级，引入新的非终结符
- 越接近开始符号 S 的文法符号优先级越低
运算结合性
- 递归非终结符在终结符左边，运算就左结合
- 如 $A \rightarrow A \beta$, $A$ 在终结符 (如 *) 左侧出现 (即终结符在 $\beta$ 中)

在 Yacc (Parser 自动生成器) 等工具中，我们可以直接指定优先级、结合性而无需自己重写文法。

%left '+'
%left '*'
%right `-`

练习: 文法的二义性

通常的符号约定

仅供参考

终结符 (Terminals, T)
- 字母表中排在前面的小写字母，如 $a、b、c$
- 运算符，如 +、* 等
- 标点符号，如括号、逗号等
- 数字 0、1、. . . 、9
- 粗体字符串，如 id, if 等
非终结符 (Nonterminals， N)
- 字母表中排在前面的大写字母，如 $A、B、 C$
- 字母 $S$. 通常表示开始符号
- 小写、斜体的名字，如 expr, stmt 等
- 代表程序构造的大写字母。如 $E$ (表达式), $T$ (项)
字母表中排在后面的大写字母 (如 $X, Y, Z$)表示文法符号（即终结符或非终结符）
字母表中排在后面的小写字母 (主要是 $u, v, \dots z$) 表示终结符号串（包括空串）
小写希腊字母，如 $\alpha, \beta, \gamma$ 表示文法符号串（包括空串）
除非特别说明，第一个产生式的左部就是开始符号

练习: 分析树构造

自顶向下的语法分析 | Top-Down Parsing👀

自顶向下的语法分析

从文法开始符号 $S$ 出发，推导出串 $w$
- 从顶部向底部方向构造 Parse Tree (从上至下，从左至右)
每一步推导需要做 两个选择
1. 替换当前句型中的哪个非终结符？
  - 自顶向下分析总是选择每个句型的 最左非终结符 进行替换!
2. 用该非终结符的哪个产生式替换？
  - 预测分析

允许回溯的递归下降分析👀

自顶向下分析的通用形式: 递归下降分析

递归下降分析 (Recursive-Descent Parsing)

由一组 过程/函数 组成，每个过程对应一个 非终结符
从开始符号 $S$ 对应的过程开始，（递归）调用其他过程
如果 $S$ 对应的过程恰好扫描了整个输入串，则分析成功

例子

question!!分析!!具体实例

已知文法 $S \rightarrow cAd$, $A \rightarrow ab \vert b$

如何为 $S$ 和 $A$ 构造其对应的过程？

利用非终结符 $A$ 的文法规则 $A \rightarrow X_1 \dots X_k$, 定义识别 $A$ 的过程

如果 $X_i$ 是非终结符：调用相应非终结符对应的过程
如果 $X_i$ 是终结符 $a$ ：匹配输入串中对应的终结符 $a$

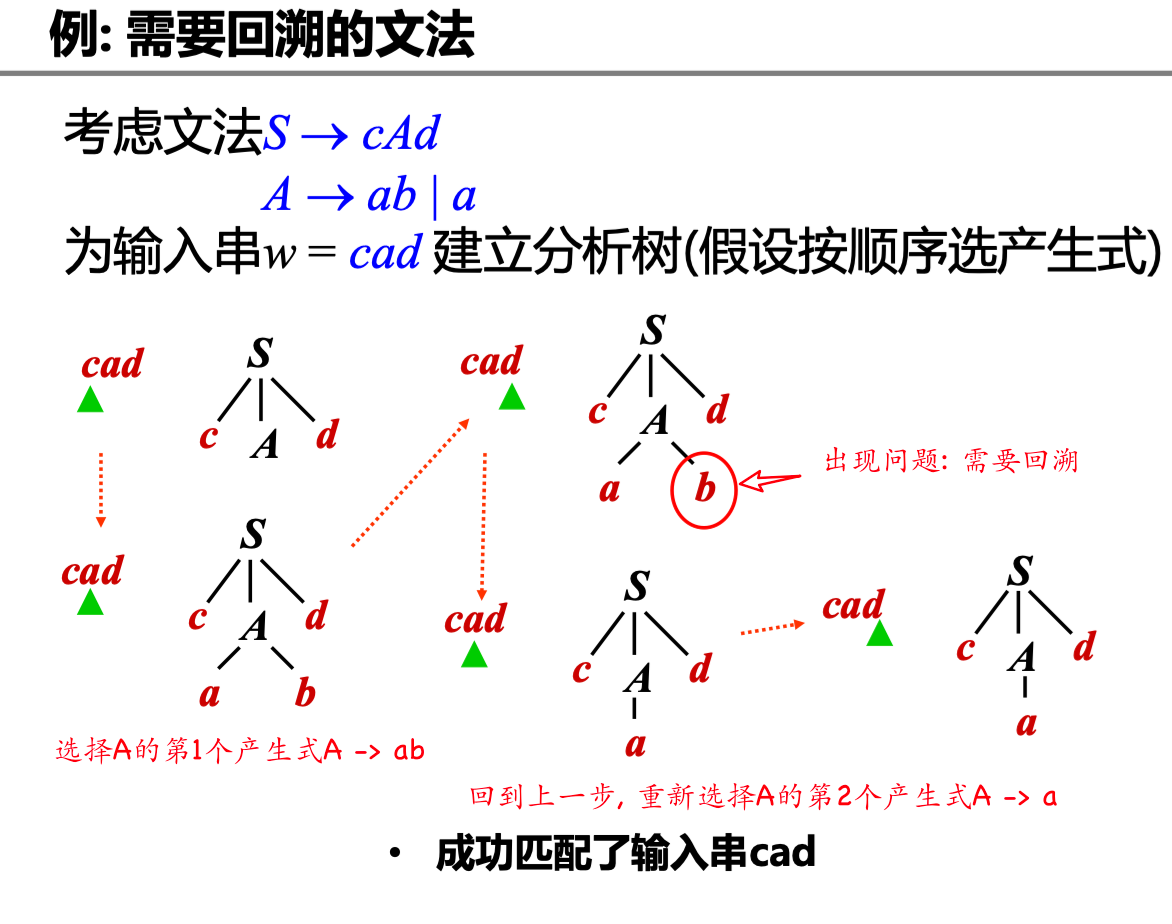
但是上述通用递归下降带来了新的问题：回溯

复杂的回溯会导致代价太高：

非终结符有可能有多个产生式，由于信息缺失，无法准确预测选择哪一个
考虑到往往需要对多个非终结符进行推导展开，因此尝试的路径可能呈指数级爆炸

其分析过程类似于 NFA，那么是否可以构造一个类似 DFA 的分析方法 -> LL(1) 分析

LL(1) 和预测分析法👀

首先给出几个定义：

预测分析法 (Predictive Parsing)

此方法接受 LL(k) 文法

第一个 L 表示从左到右扫描输入串 (Left-to-right)
第二个 L 表示最左推导 (Leftmost derivation)
k 表示向前看 k 个 Token 来确定产生式 (k 常取 1)

LL(1) 即指每次为最左边的非终结符选择产生式时，向前看 1 个输入符号，预测要使用的产生式

First 集

给定一个四元组 $G = (N, T, P, S)$, $\alpha \in (T \cup N)^*$

\[ \text{First}(\alpha) = \{a \vert \alpha \Rightarrow^* a \dots, a \in T \} \]

表示可从 $\alpha$ 推导得到的串的 首个终结符的集合

Example

龙书中关于 First 集的定义

\[ \text{First}(\alpha) = \{a \vert \alpha \Rightarrow^* a \dots, a \in T \} \cup \{\epsilon \vert \alpha \Rightarrow^* \epsilon \} \]

Follow 集

给定一个四元组 $G = (N, T, P, S)$, $A \in N$

\[ \text{Follow}(A) = \{a \vert S \Rightarrow^* \dots A a \dots, a \in T \} \]

从 $S$ 出发, 可能在推导过程中跟在 $A$ 右边的终结符号集

Example

例如：$S \rightarrow \alpha A a \beta$, 终结符号 $a \in \text{Follow}(A)$

LL(1) 文法的定义👀

LL(1) 文法判定充要条件：

文法 $G$ 的任何两个产生式 $A \rightarrow \alpha \vert \beta$ 都满足下列条件：

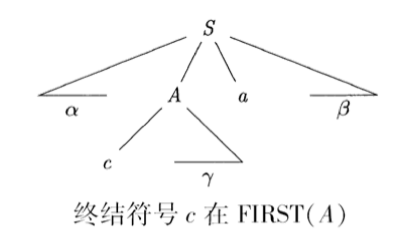
$\text{First}(\alpha) \cap \text{First}(\beta) = \emptyset$

即 $\alpha$ 和 $\beta$ 推导不出以同一个单词为首的串

Example

假设下一个输入是 $b$, 且 $\text{First}(\alpha)$ 和 $\text{First}(\beta)$ 不相交。
若 $b \in \text{First}(\alpha)$, 则选择 $A \rightarrow \alpha$; 若 $b \in \text{First}(\beta)$, 则选择 $A \rightarrow \beta$

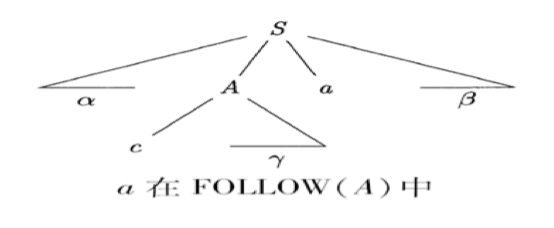
$\beta, ~ \alpha$ 至多有一个可以允许推导出空串
如果 $\beta \Rightarrow^* \epsilon$, 那么 $\alpha \nRightarrow^* \epsilon$，那么 $\text{First}(\alpha) \cap \text{Follow}(A) = \emptyset$

龙书中的不同

龙书中关于第二个条件的定义无需前面的设定，因为龙书中 First 集的定义包含了空串, 两者 First set 交集为空已经包含了 $\alpha$ 和 $\beta$ 不能同时推导出空串的情况

即

2 $\alpha$ 和 $\beta$ 不能同时推导出空串

3 如果 $\beta$ 能推导空串， $\text{First}(\alpha)$ 和 $\text{Follow}(A)$ 不能有交集

以上两条可以保证产生式选择的唯一性

Example

假设下一个输入是 $b$, 且 $\beta \Rightarrow^* \epsilon$

如果 $b \in \text{First}(\alpha)$, 选择 $A \rightarrow \alpha$ (属于条件一)
如果 $b \in \text{Follow}(A)$, 选择 $A \rightarrow \beta$，因为 $A$ 最终推导出空串且后面跟着 $b$ (属于条件二)

实现 LL(1) 预测分析👀

计算 First, Follow 集👀

由于 First, Follow 集涉及空串，这里引入 Nullable 概念

Nullable 集的归纳定义

如果 $X$ 可以推导出空串（即 $X$ 是 Nullable）, iff

Base case: $X \rightarrow \epsilon$, 那么 $X$ 显然是 Nullable
Inductive case:
- $X \rightarrow Y_1 \dots Y_n$
- 其中 $Y_1, \dots, Y_n$ 都是非终结符，且全属于 Nullable 集，那么 $X$ 也是 Nullable

龙书

虎书的 First 集合不包含 $\epsilon$
龙书不含 nullable 集，而是直接在 First 集中包含 $\epsilon$
因此在下面的计算中，X is nullable 等价于 $\epsilon \in \text{First}(X)$

根据归纳定义计算 Nullable 集

/* Nullable: a set of nonterminals */ 
Nullable <- {};
while (Nullable still changes) 
    for (each production X -> a) 
        switch (a) 
        case epsilon:
            Nullable ∪= {X}; 
            break;
        case Y1 … Yn:
            if (Y1 in Nullable && … && Yn in Nullable)
                Nullable ∪= {X}; 
            break;

First 集的归纳定义

\[ \text{First}(\alpha) = \{a \vert \alpha \Rightarrow^* a \dots, a \in T \} \]

Base case: If $X$ is a terminal -> $\text{First}(X) = \{X\}$
Inductive case: If $X \rightarrow Y_1 \dots Y_n$,
- then $\text{First}(X) \cup = \text{First}(Y_1)$
- If $Y_1$ is nullable, then $\text{First}(X) \cup = \text{First}(Y_2)$
- If $Y_1$ and $Y_2$ are both nullable, then $\text{First}(X) \cup = \text{First}(Y_3)$
- …

龙书

由于龙书的 First 集合包含 $\epsilon$, 为了和虎书的 nullable 一致性
在计算 $X \rightarrow Y_1 \dots Y_n$ 时，只有当 $Y_1, \dots, Y_n$ 都包含 $\epsilon$ 时，才将 $\epsilon$ 加入 $\text{First}(X)$

Follow 集的归纳定义

\[ \text{Follow}(A) = \{a \vert S \Rightarrow^* \dots A a \dots, a \in T \} \]

Base case: $\text{Follow}(A) = \{\}$
Inductive case: 假设存在产生式 $B \rightarrow s1 A s2$ for any s1 and s2
- $\text{Follow}(A) \cup = \text{First}(s2)$
- If $s2$ is nullable, then $\text{Follow}(A) \cup = \text{Follow}(B)$

计算 Nullable, First, Follow 集（虎书）

NullableFirstFollow

根据产生式 1，$S \rightarrow $ 可得 $S$ 是 Nullable (属于 Base case)
无 Inductive case

	nullable	FIRST	FOLLOW
S’	no
S	yes
B	no
E	no
X	no

根据产生式 1, 3, 4, 6, 7, 8, 9, 10

得到：

	nullable	FIRST
S’	no
S	yes
B	no	\
E	no	\
X	no	{, WORD, begin, end, \

根据产生式 0:
- $\text{First}(S') \cup = \text{First}(S)$
- 由于 $S$ 是 Nullable, $\text{First}(S') \cup = \text{First}(\$)$
根据产生式 2:
- $\text{First}(S) \cup = \text{First}(X)$
- $X$ 不是 Nullable，结束
根据产生式 5:
- $\text{First}(X) \cup = \text{First}(B)$
- $B$ 不是 Nullable，结束
得到:

	nullable	FIRST
S’	no	{, WORD, begin, end, \, $
S	yes	{, WORD, begin, end, \
B	no	\
E	no	\
X	no	{, WORD, begin, end, \

根据产生式 0: $\text{Follow}(S) \cup = \text{First}(\$)$
根据产生式 2:
- $\text{Follow}(X) \cup = \text{First}(S)$
- 由于 $S$ 是 Nullable, $\text{Follow}(X) \cup = \text{Follow}(S)$
根据产生式 5:
- $\text{Follow}(B) \cup = \text{First}(SE)$
- $\text{Follow}(S) \cup = \text{First}(E)$
- $\text{Follow}(E) \cup = \text{Follow}(X)$
根据产生式 6:
- $\text{Follow}(S) \cup = \text{First}(\})$

得到：

	nullable	FIRST	FOLLOW
S’	no	{, WORD, begin, end, \, $
S	yes	{, WORD, begin, end, \	\, $, }
B	no	\	{, WORD, begin, end, \
E	no	\	{, WORD, begin, end, \, $, }
X	no	{, WORD, begin, end, \	{, WORD, begin, end, \, $, }

优化 Nullable, First, Follow 的计算

构造预测分析表👀

预测分析表是指表驱动分析程序所需要的二维表 M

表的每一行 A 对应一个非终结符
表的每一列 a 对应某个终结符或输入结束符 $
表中的项 M[A, a] 表示：针对非终结符 A，当其下一个输入 Token 是 a 时，可以选择的产生式集合

构造预测分析表

对文法 $G$ 的每个产生式 $X \rightarrow \gamma$

If $t \in \text{First}(\gamma)$: enter $X \rightarrow \gamma$ into $M[X, t]$
If $\gamma$ is Nullable and $t \in \text{Follow}(X)$: enter $X \rightarrow \gamma$ into $M[X, t]$

构造预测分析表

由上面的 First, Follow 集计算结果，构造预测分析表

	nullable	FIRST	FOLLOW
S’	no	{, WORD, begin, end, \, $
S	yes	{, WORD, begin, end, \	\, $, }
B	no	\	{, WORD, begin, end, \
E	no	\	{, WORD, begin, end, \, $, }
X	no	{, WORD, begin, end, \	{, WORD, begin, end, \, $, }

产生式 0产生式 1最终预测表

$S' \rightarrow S \$$

因为 $\text{First}(S\$)$ = $, {, WORD, begin, end, \, 所以填入 $S' \rightarrow S \$$

	$	{	WORD	begin	end	\
S’	0 S’->S$	0 S’->S$	0 S’->S$	0 S’->S$	0 S’->S$	0 S’->S$
S
B
E
X

$S \rightarrow $

相当于 $\gamma$ is nullable, $\text{Follow}(S)$ = \, $, }, 所以填入 $S \rightarrow $

	$	{	WORD	begin	end	\	}
S’	0 S’->S$	0 S’->S$	0 S’->S$	0 S’->S$	0 S’->S$	0 S’->S$
S	1 S ->					1 S ->	1 S ->
B
E
X

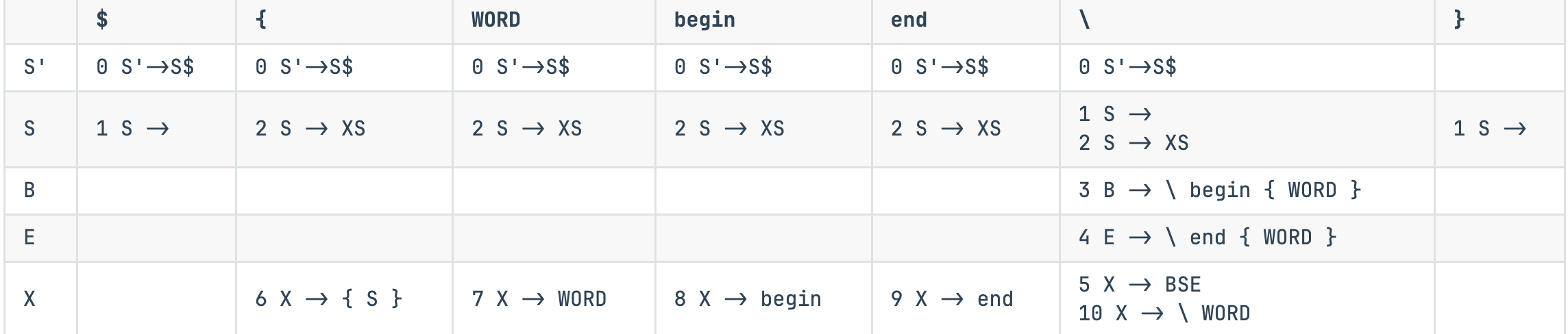
LL(1) 文法

If a predictive parsing table constructed this way contains no duplicate entries, the grammar is called LL(1)!

上述构造的预测分析表中，因为不满足每个单元格只有一个产生式的条件，所以不是 LL(1) 文法

Left-to-right parse, left-most derivation, 1 symbol lookahead

预测分析👀

LL(1) 分析的实现可以分为：

递归下降 LL(1) 分析：
- 递归下降分析: 非终结符对应子过程
非递归 LL(1) 分析 (不要求掌握)：
- 使用显式的栈，而不是递归调用来完成分析 (类似模拟下推自动机PDA)

LL(1) 的递归下降实现

递归下降语法分析程序由一组过程组成
每个非终结符号对应于一个过程
可以通过向前看一个输入符号来唯一地选择产生式

void A() {
    选择一个产生式 A -> X1 X2 ... Xn
    for (i = 1 to n) {
        if (Xi 是非终结符) {
            调用过程 Xi();
        } else if (Xi 等于当前输入符号) {
            读入下一个输入符号;
        } else {
            报错;
        }
    }
}

LL(1) 的递归下降实现

Example 1Example 2

好像这个文法和 First, Follow 没有关系，但只是因为这个文法太简单了。

For each non-terminal, the first symbols Y1 in the right-hand sides of its productions are different terminals

消除左递归、提左公因子👀

LL(1) 文法的重要性质

无二义性 | no ambiguity
无左递归 | no left recursion
无左公因子 | no left factoring

左递归 (left-recursive) 文法

如果一个文法中有非终结符号 $A$ 使得 $A \Rightarrow^+ A \alpha$, 那么称该文法是左递归的
$S \rightarrow S a \vert b$ 为直接/立即左递归

左递归文法会导致递归下降分析中的无限循环

例如：$S \rightarrow Sa \vert b$

最左推导：$S \Rightarrow Sa \Rightarrow Saa \Rightarrow \dots$

解决思路就是：限制文法或者进行文法变换

文法变换：消除直接左递归

直接左递归：$A \rightarrow A \alpha \vert \beta$
消除直接左递归：$A \rightarrow \beta A'$, $A' \rightarrow \alpha A' \vert \epsilon$ (将左递归转成右递归)

通用左递归消除方法(龙书)

一般来说

\[ S \rightarrow S ~ \alpha_1 ~ \vert ~ \dots ~ \vert ~ S ~ \alpha_n ~ \vert ~ \beta_1 ~ \vert ~ \dots ~ \vert ~\beta_m \]

可以概括所有包含左递归的情况, 可以将其改写为：

\[ \begin{aligned} &S \rightarrow \beta_1 ~ S' ~ \vert ~ \dots ~ \vert ~ \beta_m ~ S' \\ &S' \rightarrow \alpha_1 ~ S' ~ \vert ~ \dots ~ \vert ~ \alpha_n ~ S' ~ \vert ~\epsilon \end{aligned} \]

左公因子 (left-factored) 文法

如果一个文法中有非终结符号 $A$ 使得 $A \rightarrow \alpha \beta \vert \alpha \gamma$, 那么称该文法是左公因子的
会导致同一非终结符的多个候选产生式的前缀相同，导致回溯
解决思路与左递归类似：限制文法或者进行文法变换

文法变换: 提左公因子

对形如：

\[ A \rightarrow \alpha \beta \vert \alpha \gamma \]

的产生式，用如下方式 (提取相同的开始符号，并将剩下的部分用一个新的 non-terminal 来代替) 改写：

\[ \begin{aligned} &A \rightarrow \alpha A' \\ &A' \rightarrow \beta \vert \gamma \end{aligned} \]

其中 $A'$ 是新的非终结符

通过改写产生式来推迟决定，等读入了足够多的输入，获得足够信息后再做选择

错误恢复 | Error Recovery👀

经过前面的步骤构建了预测分析表后, 预测表中的空单元格 (blank entry) 表示一个语法错误 (syntax error)

e.g., $M[T, x] = \emptyset$ indicates that the parsing function $T()$ does not expect to see token $x$ - this is a syntax error

遇到错误的时候如何解决？

Raise an exception and quit parsing (safe but not user-friendly)
print an error message and recover from the error (more user-friendly, other syntax errors can be found in the same compilation)

Raise and Quit👀

void T() {
    switch (token) {
        case ID: 
        case NUM:
        case LPAREN: F(); Tprime(); break;
        default:
            error();
    }
}

Print and Recover👀

A syntax error occurs when the string of input tokens is not a sentence in the language. Error recovery is a way of finding some sentence similar to that string of tokens.
This can proceed by deleting, replacing, or inserting tokens.
Through inserting: pretend we have the token and return normally

void T( ) {
    switch (tok) { 
        case ID: 
        case NUM: 
        case LPAREN: F( ); Tprime( ); break; 
        default: print("expected id, num, or left-paren"); 
    }
}

做插入比较危险，if the error cascades to produce another error, the process might loop indefinitely

Deleting tokens is safer, because the loop must eventually terminate when EOF is reached
Simple recover by deletion works by skipping tokens util a token in the $\text{FOLLOW}$ set is reached.

int Tprime_follow [ ] = {PLUS, TIMES, RPAREN, EOF, -1}; 
void Tprime( ) { 
    switch (tok) { 
        case PLUS: break; 
        case TIMES: eat(TIMES); F(); Tprime(); break; 
        case RPAREN: break; 
        case EOF: break; 
        default: 
            print("expected +, *, right-paren, or end-of-file"); 
            skipto(Tprime_follow);
    }
}

David G. Cantor. 1962. On The Ambiguity Problem of Backus Systems. J. ACM 9, 4 (Oct. 1962), 477–479. ↩

本文总阅读量: 次