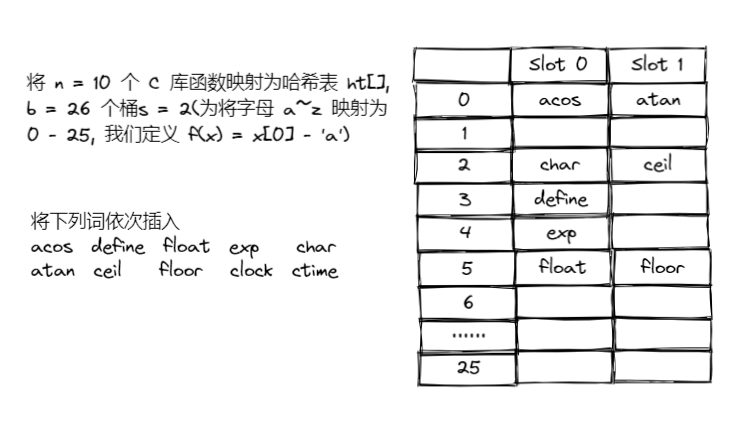
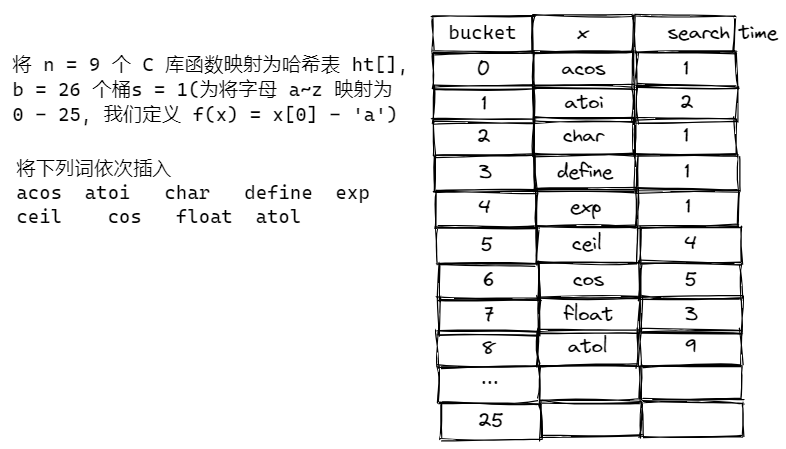
哈希 | Hash👀

约 1120 个字 120 行代码预计阅读时间 5 分钟

Abstract

重点: 设计哈希函数 + 如何解决冲突

哈希表 | 散列表👀

哈希表把关键字 (或标识符 | identifier) 值映射到表中一个位置
- 支持查询、插入、删除等操作
对于标识符 $x$ , 定义一个哈希函数 $f(x) = x$ 在哈希表 ht[] 中的位置
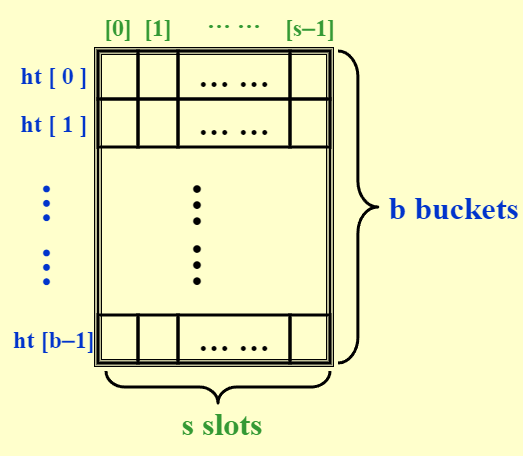
- 如图, ht 的大小为 $b$（即 $f(x)$ 值域为 $[0, b-1]$），最多有 s 个槽
- $T$ = $x$ 可能的不同值的个数
- $n$ = ht 中不同标识符的个数
- 标识符密度 (identifier density) = $n/T$
- 装载密度 (loading density) = $\lambda = n/(sb)$
冲突 (collision) ——> 当将两个不同的标识符散列到同一个桶中时 (i.e. $i_1 \neq i_2$ 但 $f(i_1) = f(i_2)$ )
溢出（overflow）: 当将一个新的标识符散列到一个满的桶时

当 s = 1 时，碰撞和溢出将同时发生
没有溢出时，$T_{search} = T_{insert} = T_{delete} = O(1)$

Example

哈希函数👀

Properties of f()

函数必须易于计算且尽量减少碰撞的可能性
函数应该是公正的 (unbiased)，即对任意 $x$ 和 $i$ 都有 $Probability(f(x) = i) = 1/b$ . 这种函数称为均匀哈希函数（uniform hash function）

几种函数构造方法:

除留余数法 —— $f(x) = x ~~ \% ~~ TableSize;$ /* if x is an integer*/
- TableSize 最好选择一个质数 —— good for random integer keys
Example

关键字内部代码 key MOD 100

key1 511 11

key2 512 12

key3 411 11
平方取中法 —— 先计算关键字值的平方，然后取平方值的中间几位作为散列地址

Example

关键字内部代码内部代码平方 hash(key)

key1 511 261121 11

key2 512 262144 21

key3 411 168921 89
折叠法 —— 将关键字分为位数相同的几部分，然后取这几部分的叠加和（舍去进位）作为散列地址 (用于关键字位数较多，并且关键字中每一位上数字分布大致均匀)

Example
数字分析法 —— 当关键字的位数大于地址的位数，对关键字的各位分布进行分析，选出分布均匀的任意几位作为散列地址 (适用于所有关键字都已知的情况下，根据实际应用确定要选取的部分，尽量避免发生冲突)

Example

比如按学号映射，同届前几位相同，将后四位选为 key
$f(x) = (\sum x[i]) ~~ \% ~~ TableSize;$ /* if x is a string*/

Example

$x = "abc" \Rightarrow \sum x[i] = 'a' + 'b' + 'c'$
$f(x) = (x[0] + x[1] * 27 + x[2] * 27^2 ) ~~ \% ~~ TableSize;$ /* 变成 27 进制 */

$f(x) = (\sum x[N-i-1] * 32^i) ~~ \% ~~ TableSize$ /* *32 可以变为移位运算 */

Example

Index Hash3(const char *x, int TableSize)
{
    unsigned int HashVal = 0;
    while(*x != '\0')
    {
        HashVal = (HashVal << 5) + *x++;
    }
    return HashVal % TableSize;
}

解决冲突👀

分离链接 | Separate Chaining👀

将散列到相同值的元素保存在一个列表（链表）中

code

struct  ListNode; 
typedef  struct  ListNode  *Position; 
struct  HashTbl; 
typedef  struct  HashTbl  *HashTable; 
struct  ListNode { 
    ElementType  Element; 
    Position  Next; 
}; 
typedef  Position  List; 
/* List *TheList will be an array of lists, allocated later */ 
/* The lists use headers (for simplicity), */ 
/* though this wastes space */ 
struct  HashTbl { 
    int  TableSize; 
    List  *TheLists; 
};

Create an empty table

HashTable  InitializeTable( int TableSize ) 
{   HashTable  H; 
    int  i; 
    if ( TableSize < MinTableSize ) 
    { 
        Error( "Table size too small" );  
        return NULL;  
    } 
    H = malloc( sizeof( struct HashTbl ) );  /* Allocate table */
    if ( H == NULL )    
        FatalError( "Out of space!!!" ); 
    H->TableSize = NextPrime( TableSize );  /* Better be prime */
    H->TheLists = malloc( sizeof( List ) * H->TableSize );  /*Array of lists*/
    if ( H->TheLists == NULL )   
        FatalError( "Out of space!!!" ); 
    for( i = 0; i < H->TableSize; i++ ) 
    {   /* Allocate list headers */
        H->TheLists[ i ] = malloc( sizeof( struct ListNode ) ); /* Slow! */
        if ( H->TheLists[ i ] == NULL )  
            FatalError( "Out of space!!!" ); 
        else    
            H->TheLists[ i ]->Next = NULL;
    } 
    return  H; 
}

Find a key from a hash table

Position  Find ( ElementType Key, HashTable H ) 
{ 
    Position P; 
    List L; 

    L = H->TheLists[ Hash( Key, H->TableSize ) ]; 

    P = L->Next; 
    while( P != NULL && P->Element != Key )  /* Probably need strcmp */ 
        P = P->Next; 
    return P; 
}

Insert a key into a hash table

void  Insert ( ElementType Key, HashTable H ) 
{ 
    Position   Pos, NewCell; 
    List  L; 
    Pos = Find( Key, H ); 
    if ( Pos == NULL ) 
    {   /* Key is not found, then insert */
        NewCell = malloc( sizeof( struct ListNode ) ); 
        if ( NewCell == NULL )     
            FatalError( "Out of space!!!" ); 
        else 
        { 
            L = H->TheLists[ Hash( Key, H->TableSize ) ]; 
            NewCell->Next = L->Next; 
            NewCell->Element = Key; /* Probably need strcpy! */ 
            L->Next = NewCell; 
        } 
    } 
}

Tips: 将 TableSize 的大小设置为预期 keys 的数量几乎一样 (i.e. 使得装载密度 $\lambda \approx 1 $)

开放地址 | Open Adressing👀

当有冲突发生时，选择下一个位置，直到找到空的为止
即有多个哈希函数 $h_0(x), h_1(x), \cdots$，其中 $h_i(x) = (\mathrm{hash}(x)+f(i)) ~~ \% ~~ TableSize$
- 其中 $f(i)$ 为增量函数，有多种选取的方式
通常情况下 $\lambda < 0.5$ , 如果大于 0.5 就会引发大量的冲突

void insert(int key) {
    index = hash(key);
    int i = 0;  // the counter of probing
    while (collision at index) {
        index = (hash(key) + f(i)) % TableSize;
        if (table is full) 
            break;
        else 
            i++;
    }
    if (table is full) 
        Error("No space left");
    else 
        insert key at index;
}

线性探测 | Linear Probing
- 增量函数 $f(i) = i$ —— 会导致初次聚集（primary clustering），即一旦发生了冲突，那么后面的元素都会聚集在一起，搜索次数会变得越来越大
- 使用线性探测的探测次数对于插入和不成功查找来说约为$\dfrac{1}{2}\left(1+\dfrac{1}{(1-\lambda)^2}\right)$
- 对于成功的查找来说则需要 $\dfrac{1}{2}\left(1+\dfrac{1}{1-\lambda}\right)$ 次
Example

Average search time = 27 / 9 = 3
二次探测 | Quadratic Probing
- 增量函数 $f(i) = i^2$ —— 避免了 primary clustering, 但是导致有可能有空位但就是找不到
- 若使用平方探测（或二次探测）, 且表的大小是素数，那么当表至少有一半是空的时候，总能插入一个新的元素
  
  一些改进: If the table size is a prime of the form $4k + 3$ , then the quadratic probing $f(i) = \pm ~~ i^2$ can probe the entire table.
  Find
```
Position  Find ( ElementType Key, HashTable H ) 
{   
    Position  CurrentPos; 
    int  CollisionNum; 
    CollisionNum = 0; 
    CurrentPos = Hash( Key, H->TableSize ); 
    while( H->TheCells[ CurrentPos ].Info != Empty && H->TheCells[ CurrentPos ].Element != Key ) 
    { 
        CurrentPos += 2 * ++CollisionNum - 1;  // h = h + 2i - 1
        if ( CurrentPos >= H->TableSize )  
            CurrentPos -= H->TableSize;   
    } 
    return CurrentPos; 
} 
```
  Insert
```
void  Insert ( ElementType Key, HashTable H ) 
{ 
    Position  Pos; 
    Pos = Find( Key, H ); 
    if ( H->TheCells[ Pos ].Info != Legitimate ) 
    { /* OK to insert here */ 
        H->TheCells[ Pos ].Info = Legitimate; 
        H->TheCells[ Pos ].Element = Key; /* Probably need strcpy */ 
    } 
} 
```
1. 双重哈希 | Double Hashing —— 即 $f(i) = i \times hash_2(x)$; /* hash2(x) 是第二个 hash 函数 */
  - 一般选择 $hash_2(x) = R - (x ~~ \% ~~ R)$ ($R$ 为小于表大小的质数) 效果更好
  - 如果正确实现了双重哈希，模拟显示预期的探测次数几乎与随机冲突解决策略相同
  - 二次探测不需要使用第二个哈希函数，在实践中更简单快速
2. 再哈希:
  - 使用二次探测，如果表的元素填的过满 (大约是装载密度 > 0.5 时)，那么操作时间会过长，且 Insert 可能失败，这可能发生在有太多的移动和插入混合的场合
  - 解决方法是再哈希:
    - 建立另外一个大约两倍大的表且使用一个相关的新哈希函数
    - 扫描整个原始哈希表
    - 计算每个(未删除的)元素的新哈希值并将其插入到新表中
  - 如果表中有 N 个元素，那再哈希的时间复杂度 $T(N) = O(N)$
  - 什么时候再哈希
    - 只要表有一半满
    - 插入操作失败时
    - 当表达到一个特定的装载密度

本文总阅读量: 次

关键字	内部代码	key MOD 100
key1	511	11
key2	512	12
key3	411	11

关键字	内部代码	内部代码平方	hash(key)
key1	511	261121	11
key2	512	262144	21
key3	411	168921	89