跳转至

图 | Graph👀

约 2019 个字 591 行代码 预计阅读时间 14 分钟

Definitions👀

  1. Length of a path: 路径上边的数目
  2. Simple path: Path 中的点 vi1, vi2, ···, vin 都不同
  3. 无向图
    1. connected: 若存在一条从 vi 到 vj 的路径，则称 vi 和 vj 连通
    2. connected graph: 任意点之间都连通，称无向图是连通的
    3. connected component: 无向图的极大连通子图
  4. tree: 连通的无环图
  5. DAG: directed acyclic graph | 有向无环图
  6. Strongly connected component: 有向图的极大强连通子图
  7. Degree(v):
    1. 对有向图，度分为入度和出度
    2. 对无向图，度数是与其相邻的节点数
    3. 边数等于所有节点的度数和除以 2

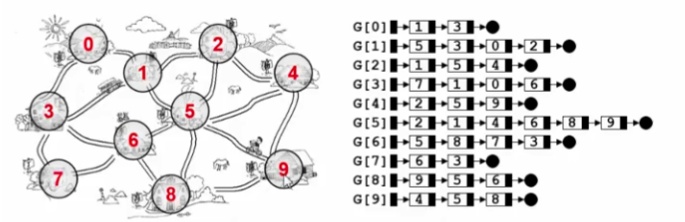
图的表示👀

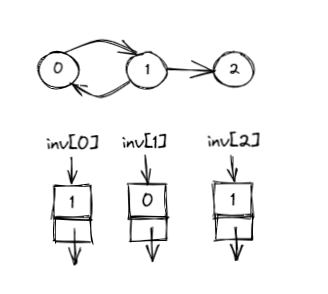
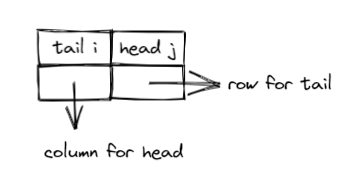
  1. 邻接矩阵 G[N][N] —— N 个顶点从 0 到 N-1 编号
    • G[i][j] = < vi, vj > 是 G 中的边 ? 1 : 0

Tip

  • 对于无向图的存储，用一个长度为 N(N+1)/2 的一维数组 A 存储 {G00, G10, G11, ···, G(n-1)0, ···, G(n-1)(n-1)}, 则 Gij 在 A 中对应的下标是: i * (i + 1) / 2 + j
  • 对于网络，只要把 G[i][j] 的值定义为边 < vi, vj > 的权重即可
  1. 邻接表表示法 —— G[N] 为指针数组，对应矩阵每行要给链表且只存非 0 元素
    2023-01-30-16-55-50
    • 对于无向图，每个边会被存储两次
    • 对于有向图，无法遍历入度，如果要查询入度可采用以下两种方法:
      • 增加逆邻接表
        2023-01-30-17-15-48
      • 采用多重链表
        2023-01-30-17-19-04

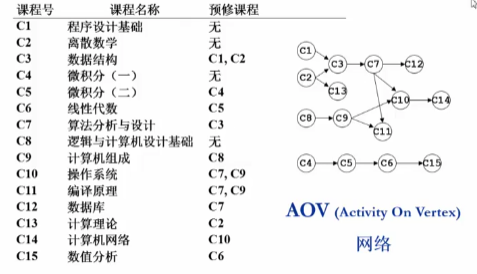
拓扑排序👀

Abstract

  • AOV 网络 —— 定点表示活动，边表示先后关系
  • 若存在一条从 i 到 j 的路径，则称 i 为 j 的前驱 (predecessor), j 是 i 的后继 (successor)
  • 若存在一条边 < i, j >，则称 i 是 j 的直接前驱 (immediate predecessor) ，j 是 i 的直接后继

拓扑序👀

  • 若在图中从 V 到 W 有一条有向路径，则 V 一定排在 W 之前。满足此条件的顶点序列称为一个拓扑序 (获得一个拓扑序的过程就是拓扑排序)
  • AOV 如果有合理的拓扑序，则必定是有向无环图 (Directed Acyclic Graph, DAG)

    2023-01-30-18-22-40
    如果有向图中出现环，一定不可能得到一个合理的拓扑序

拓扑排序算法👀

void Topsort(Graph G)
{
      int Counter;
      Vertex V, W;
      for(Counter = 0; Counter < NumVertex; Counter ++)
      {
            V = FindNeVertexOfDegreeZero();     /* O(|V|) */
            if(V == NotAVertex)
            {
                  Error("Graph has a cycle");
                  break;
            }
            TopNum[V] = Counter;    /*or output V*/
            for(each W adjacent to V)
                  Indegree[W] --;
      }
}
  • 上述算法的时间复杂度 $T = O(|V|^2) $
  • Improvement: 随时将入度变为 0 的顶点放到一个容器中(栈或队列等)
Improvement
void Topsort( Graph G )
{   
      Queue  Q;
      int  Counter = 0;
      Vertex  V, W;
      Q = CreateQueue( NumVertex );  
      MakeEmpty( Q );
      for ( each vertex V )
            if ( Indegree[ V ] == 0 )   
                  Enqueue( V, Q );
      while ( !IsEmpty( Q ) )
      {
            V = Dequeue( Q );
            TopNum[ V ] = ++ Counter; /* assign next */
            for ( each W adjacent to V )
                  if ( – – Indegree[ W ] == 0 )  
                        Enqueue( W, Q );
      }  /* end-while */
      if ( Counter != NumVertex )
            Error( “Graph has a cycle” );

      DisposeQueue( Q ); /* free memory */}

若有环则一定会存在找不到入度为 0 的点，来进入构成环的子图

邻接表存储—拓扑排序算法 
bool TopSort( LGraph Graph, Vertex TopOrder[] )
{ /* 对Graph进行拓扑排序,  TopOrder[]顺序存储排序后的顶点下标 */
int Indegree[MaxVertexNum], cnt;
Vertex V;
PtrToAdjVNode W;
Queue Q = CreateQueue( Graph->Nv );

/* 初始化Indegree[] */
for (V=0; V<Graph->Nv; V++)
      Indegree[V] = 0;

/* 遍历图，得到Indegree[] */
for (V=0; V<Graph->Nv; V++)
      for (W=Graph->G[V].FirstEdge; W; W=W->Next)
            Indegree[W->AdjV] ++; /* 对有向边<V, W->AdjV>累计终点的入度 */

/* 将所有入度为0的顶点入列 */
for (V=0; V<Graph->Nv; V++)
      if ( Indegree[V]==0 )
            AddQ(Q, V);

/* 下面进入拓扑排序 */ 
cnt = 0; 
while( !IsEmpty(Q) ){
      V = DeleteQ(Q); /* 弹出一个入度为 0 的顶点 */
      TopOrder[cnt ++] = V; /* 将之存为结果序列的下一个元素 */
      /* 对V的每个邻接点W->AdjV */
      for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( --Indegree[W->AdjV] == 0 )/* 若删除V使得W->AdjV入度为0 */
                AddQ(Q, W->AdjV); /* 则该顶点入列 */ 
} /* while结束*/

if ( cnt != Graph->Nv )
      return false; /* 说明图中有回路, 返回不成功标志 */ 
else
      return true;
}

最短路算法👀

最短路径问题的抽象

在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径。这条路径即两点之间的最短路径 (Shortest Path) , 第一个顶点为源点 (Source) , 最后一个顶点为终点 (Destination)

问题分类👀

  1. 单源最短路径: 从固定源点出发，求其到所有其他顶点的最短路径
    1. (有向) 无权图
    2. (有向) 有权图
  2. 多源最短路径: 求任意两顶点间的最短路径

无权图的单源最短路👀

按照递增 (递减) 的顺序找出到各顶点的最短路
采用 BFS (Breadth-first search)

Implementation

Table[i].Dist = distance from s to vi  /* initialized to be Infinity except for s */
Table[i].Known = 1 if vi is checked; or 0 if not
Table[ i ].Path = for tracking the path   /* initialized to be 0 */
  1. Normal:
    void Unweighted( Table T )
{   
    int  CurrDist;
    Vertex  V, W;
    for ( CurrDist = 0; CurrDist < NumVertex; CurrDist ++ ) 
    {
        for ( each vertex V )
            if ( !T[ V ].Known && T[ V ].Dist == CurrDist ) 
            {
                T[ V ].Known = true;
                for ( each W adjacent to V )
                    if ( T[ W ].Dist == Infinity ) 
                    {
                        T[ W ].Dist = CurrDist + 1;
                        T[ W ].Path = V;
                    } /* end-if Dist == Infinity */
            } /* end-if !Known && Dist == CurrDist */
    }  /* end-for CurrDist */
}

    \(T = O(|V|^2)\)

  2. Improvement:
    void Unweighted( Table T )
{   /* T is initialized with the source vertex S given */
    Queue  Q;
    Vertex  V, W;
    Q = CreateQueue (NumVertex );  
    MakeEmpty( Q );
    Enqueue( S, Q ); /* Enqueue the source vertex */
    while ( !IsEmpty( Q ) ) 
    {
        V = Dequeue( Q );
        T[ V ].Known = true; /* not really necessary */
        for ( each W adjacent to V )
            if ( T[ W ].Dist == Infinity ) 
            {
                T[ W ].Dist = T[ V ].Dist + 1;
                T[ W ].Path = V;
                Enqueue( W, Q );
            } /* end-if Dist == Infinity */
    } /* end-while */
    DisposeQueue( Q ); /* free memory */
}

    \(T = O(|V|+|E|)\)

邻接表存储 - 无权图的单源最短路算法 
/* dist[]和path[]全部初始化为-1 */
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{
    Queue Q;
    Vertex V;
    PtrToAdjVNode W;

    Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */
    dist[S] = 0; /* 初始化源点 */
    AddQ (Q, S);

    while( !IsEmpty(Q) ){
        V = DeleteQ(Q);
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
            if ( dist[W->AdjV]==-1 ) { /* 若W->AdjV未被访问过 */
                dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */
                path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */
                AddQ(Q, W->AdjV);
            }
    } /* while结束*/
}

有权图的单源最短路👀

按照递增的顺序找出到各顶点的最短路

Dijkstra 算法👀

  • 令 S = {源点 s + 已经确定了最短路径的顶点 vi }
  • 对任一未收录的顶点 v, 定义 dist[v] 为 s 到 v 的最短路径长度，但该路径仅经过 s 中的顶点。
  • 由于路径按照递增顺序生成
    • 真正的最短路必须只经过 S 中的顶点
    • 每次从未收录的顶点中选一个 dist 最小的收录
    • 增加一个 v 进入 S，可能影响另一个 w 的 dist 值(dist[w] = min{dist[w], dist[v] + < v, w > 的权重})

code

伪码
void Dijkstra(Table T)
{
      Vertex V, W;
      for(;;)     /* O(|V|) */
      {
            V = smallest unknown distance vertex;
            if(V == NotAVertex)
                  break;
            T[V].Known = true;
            for(each W adjacent to V)
                  if(!T[W].Known)
                        if(T[V].Dist + Cvw < T[W].Dist)
                        {
                            Decrease(T[W].Dist to T[V].Dist + Cvw);
                            T[W].Path = V;
                        }/* end-if update W */
      }/* end-for(;;) */
}
/* 不能解决有负边的情况 */
Dijkstra算法的声明 
typedef int Vertex;
struct TableEntry
{
      List Header;      /* Adjacency list */
      int Known;
      DistType Dist;
      Vertex Path;
};
/* Vertices are numbered from 0 */
#define NotAVertex (-1)
typedef struct TableEntry Table[NumVertex];
表初始化例程 
void InitTable(Vertex Start, Graph G, Table T)
{
      int i;
      ReadGraph(G, T);  /* Read graph somehow */
      for(i = 0; i < NumVertex; i++)
      {
            T[i].Known = False;
            T[i].Dist = Infinity;
            T[i].Path = NotAVertex;
      }
      T[Start].dist = 0;
}
显示实际最短路径的例程 
/* Print shortest path to V after Dijkstra has run */
/* Assume that the path exists */
void PrintPath(Vertex V, Table T)
{
      if(T[V].Path != NotAVertex)
      {
            PrintPath(T[V].Path, T);
            printf(" to");
      }
      printf("%v", V);  // %v 是伪代码
}
  • 因为判定条件 T[V].Dist + Cvw < T[W].Dist，T[i].Dist 要初始化为正无穷
  • 优化如下：
    • Implementation 1: 直接扫描所有未收录顶点 —— \(O(|V|)\)
      • \(T = O(|V|^2 + |E|)\) —— 对于稠密图效果好
    • Implementation 2: 将 dist 存在最小堆中 —— \(O(log|V|)\)
      • 更新 T[W].Dist 的值 —— \(O(log|V|)\)
      • $ T = O(|V|log|V| + |E|log|V|) = O(|E|log|V|) $ —— 对稀疏图效果好(指 V 和 E 一个数量级)
邻接矩阵存储 - 有权图的单源最短路算法 
Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ 
    /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    int MinDist = INFINITY;

    for (V=0; V<Graph->Nv; V++) 
    {
        if ( collected[V]==false && dist[V]<MinDist) 
        {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else 
        return ERROR;  /* 若这样的顶点不存在，返回错误标记 */
}

bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
    int collected[MaxVertexNum];
    Vertex V, W;

    /* 初始化：此处默认邻接矩阵中不存在的边用 INFINITY 表示 */
    for ( V=0; V<Graph->Nv; V++ ) {
        dist[V] = Graph->G[S][V];
        if ( dist[V] < INFINITY )
            path[V] = S;
        else
            path[V] = -1;
        collected[V] = false;
    }
    /* 先将起点收入集合 */
    dist[S] = 0;
    collected[S] = true;

    while (1) {
        /* V = 未被收录顶点中 dist 最小者 */
        V = FindMinDist( Graph, dist, collected );
        if ( V == ERROR ) /* 若这样的V不存在 */
            break;      /* 算法结束 */
        collected[V] = true;  /* 收录V */
        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            /* 若W是V的邻接点并且未被收录 */
            if ( collected[W]==false && Graph->G[V][W]<INFINITY ) 
            {
                if ( Graph->G[V][W]<0 ) /* 若有负边 */
                    return false; /* 不能正确解决，返回错误标记 */
                /* 若收录V使得dist[W]变小 */
                if ( dist[V]+Graph->G[V][W] < dist[W] ) {
                    dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
                    path[W] = V; /* 更新S到W的路径 */
                }
            }
    } /* while结束*/
    return true; /* 算法执行完毕，返回正确标记 */
}

带负权图👀

时间复杂度 \(T = O(|V| \times |E|)\)

void  WeightedNegative( Table T )
{   
    Queue  Q;
    Vertex  V, W;
    Q = CreateQueue (NumVertex );  
    MakeEmpty( Q );
    Enqueue( S, Q ); /* Enqueue the source vertex */
    while ( !IsEmpty( Q ) ) 
    {
        V = Dequeue( Q );   /* each vertex can dequeue at most |V| times */
        for ( each W adjacent to V )
            if ( T[ V ].Dist + Cvw < T[ W ].Dist )  /* no longer once per edge */
            {
                T[ W ].Dist = T[ V ].Dist + Cvw;
                T[ W ].Path = V;
                if ( W is not already in Q )
                    Enqueue( W, Q );
            } /* end-if update */
    } /* end-while */
    DisposeQueue( Q ); /* free memory */
}
/* negative-cost cycle will cause indefinite loop */

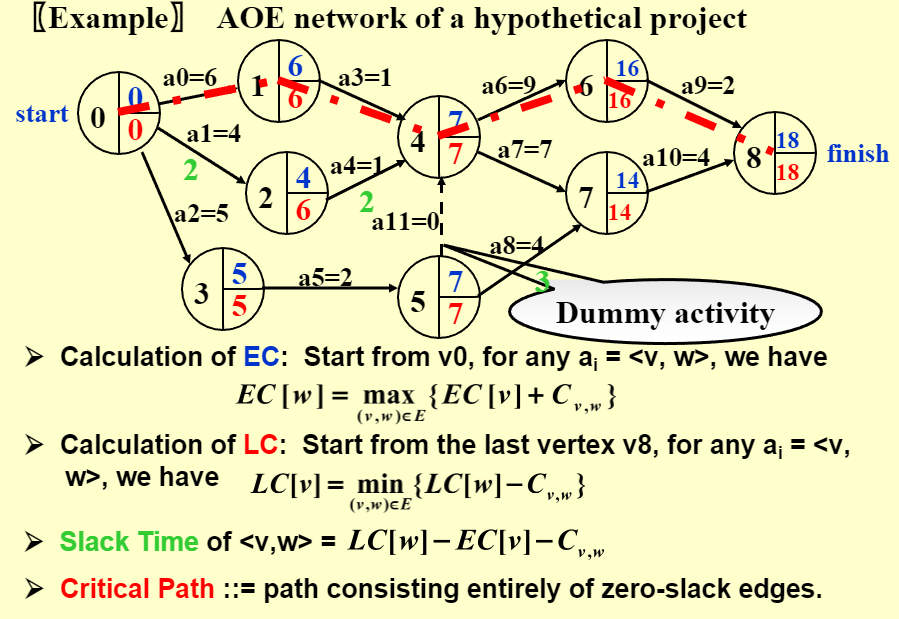
无环图 | Acyclic Graph👀

此部分主要是其在 AOE (Activity On Edge) 网络的应用
一般用于安排项目的工序

  • 每个结点存储一个最早完成时间和最晚完成时间
  • 每条边存在一个持续时间 (边权 C ) 和一个松弛时间
  • 相关计算:
    • EC (earliest completion): 最早完成时间，从前往后计算
    • LC (latest completion): 最晚完成时间，用需要最长的时间从后向前依次减去
    • Slack Time: 松弛时间 | 机动时间，最早完成的时间和要求的最晚完成的时间之间的时间
    • Critical Path: 关键路径，可能不止一条但找出一条路径上所有点都是关键点（松弛时间为 0）的就行
Quote

2023-01-31-22-04-18

图片摘自课程PPT

CSDN-AOE网络(大力海棠的博客)

拓展

多源最短路

算法——(直接将单源最短路算法调用 |V| 遍 or Floyd 算法)

Floyd 算法
void Floyd()
{
    for( i = 0; i < N; i++)
    {
        for( j = 0; j < N; j++)
        {
            D[i][j] = G[i][j];
            path[i][j] = -1;
            /*path用于记录路径*/
        }
    }
    for( k = 0; k < N; k++)
    {
        for( i = 0; i < N; i++)
        {
            for( j = 0; j < N; j++)
            {
                if( D[i][k] + D[k][j] < D[i][j])
                {
                    D[i][j] = D[i][k] + D[k][j];
                    path[i][j] = k;
                    /*如果将i到j的最短路径*/
                }
            }
        }
    }
}

最小生成树 | Minimum Spanning Tree👀

  • 是一棵树，且：
    • 无回路
    • 连通的
    • |V|个顶点一定有|V| -1条边
  • 是生成树
    • 包含全部顶点
    • |V| -1条边都在图中
  • 边的权重和最小

向生成树中任加一条边都一定构成回路
最小生成树存在 \(\Leftrightarrow\) 图连通

Prim 算法👀

稠密图一般用此算法，每次寻找的是和已经收罗进最小生成树所有顶点相邻的边
类似 Dijkstra 算法, \(T = O( |V| ^2 )\)

code
邻接矩阵存储
/* 邻接矩阵存储 - Prim最小生成树算法 */

Vertex FindMinDist( MGraph Graph, WeightType dist[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    WeightType MinDist = INFINITY;

    for (V=0; V<Graph->Nv; V++) 
    {
        if ( dist[V]!=0 && dist[V]<MinDist) 
        {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else 
        return ERROR;  /* 若这样的顶点不存在，返回-1作为标记 */
}

int Prim( MGraph Graph, LGraph MST )
{ 
    /* 将最小生成树保存为邻接表存储的图 MST，返回最小权重和 */
    WeightType dist[MaxVertexNum], TotalWeight;
    Vertex parent[MaxVertexNum], V, W;
    int VCount;
    Edge E;

    /* 初始化。默认初始点下标是0 */
    for (V=0; V<Graph->Nv; V++) {
        /* 这里假设若V到W没有直接的边，则Graph->G[V][W]定义为INFINITY */
        dist[V] = Graph->G[0][V];
        parent[V] = 0; /* 暂且定义所有顶点的父结点都是初始点0 */ 
    }
    TotalWeight = 0; /* 初始化权重和     */
    VCount = 0;      /* 初始化收录的顶点数 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 */

    /* 将初始点0收录进MST */
    dist[0] = 0;
    VCount ++;
    parent[0] = -1; /* 当前树根是0 */

    while (1) {
        V = FindMinDist( Graph, dist );
        /* V = 未被收录顶点中dist最小者 */
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;   /* 算法结束 */

        /* 将V及相应的边<parent[V], V>收录进MST */
        E->V1 = parent[V];
        E->V2 = V;
        E->Weight = dist[V];
        InsertEdge( MST, E );
        TotalWeight += dist[V];
        dist[V] = 0;
        VCount++;

        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            if ( dist[W]!=0 && Graph->G[V][W]<INFINITY ) {
            /* 若W是V的邻接点并且未被收录 */
                if ( Graph->G[V][W] < dist[W] ) {
                /* 若收录V使得dist[W]变小 */
                    dist[W] = Graph->G[V][W]; /* 更新dist[W] */
                    parent[W] = V; /* 更新树 */
                }
            }
    } /* while结束*/
    if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */
    TotalWeight = ERROR;
    return TotalWeight;   /* 算法执行完毕，返回最小权重和或错误标记 */
}

Kruskal 算法👀

将每个顶点都看作一棵树，收集的是边，如果这条边收入构成回路就不收入，如果不构成就收入（从边权重最小开始收，收到边的数量为|V|-1为止）

  • 稀疏图一般用此算法（边的数量和顶点数量级差不多）
  • \(T = O(|E|log|E|)\)
伪码
void Kruskal ( Graph G )
{   
    T = { } ;
    while ( T contains less than |V| 1 edges && E is not empty ) 
    {
        choose a least cost edge (v, w) from E ;    /* DeleteMin */
        delete (v, w) from E ;
        if  ( (v, w) does not create a cycle in T )     
            add (v, w) to T ;   /* Union / Find */
        else
            discard (v, w) ;
    }
    if( T contains fewer than |V| - 1 edges )
        Error ( “No spanning tree” ) ;}
code
邻接矩阵存储
/* 邻接表存储 - Kruskal最小生成树算法 */

/*-------------------- 顶点并查集定义 --------------------*/
typedef Vertex ElementType; /* 默认元素可以用非负整数表示 */
typedef Vertex SetName;     /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */

void InitializeVSet( SetType S, int N )
{ /* 初始化并查集 */
    ElementType X;

    for ( X=0; X<N; X++ ) S[X] = -1;
}

void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
    /* 保证小集合并入大集合 */
    if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
        S[Root2] += S[Root1];     /* 集合1并入集合2  */
        S[Root1] = Root2;
    }
    else {                         /* 如果集合1比较大 */
        S[Root1] += S[Root2];     /* 集合2并入集合1  */
        S[Root2] = Root1;
    }
}

SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] ); /* 路径压缩 */
}

bool CheckCycle( SetType VSet, Vertex V1, Vertex V2 )
{ /* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
    Vertex Root1, Root2;

    Root1 = Find( VSet, V1 ); /* 得到V1所属的连通集名称 */
    Root2 = Find( VSet, V2 ); /* 得到V2所属的连通集名称 */

    if( Root1==Root2 ) /* 若V1和V2已经连通，则该边不能要 */
        return false;
    else { /* 否则该边可以被收集，同时将V1和V2并入同一连通集 */
        Union( VSet, Root1, Root2 );
        return true;
    }
}
/*-------------------- 并查集定义结束 --------------------*/

/*-------------------- 边的最小堆定义 --------------------*/
void PercDown( Edge ESet, int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p )    */
/* 将N个元素的边数组中以ESet[p]为根的子堆调整为关于Weight的最小堆 */
    int Parent, Child;
    struct ENode X;

    X = ESet[p]; /* 取出根结点存放的值 */
    for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if( (Child!=N-1) && (ESet[Child].Weight>ESet[Child+1].Weight) )
            Child++;  /* Child指向左右子结点的较小者 */
        if( X.Weight <= ESet[Child].Weight ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            ESet[Parent] = ESet[Child];
    }
    ESet[Parent] = X;
}

void InitializeESet( LGraph Graph, Edge ESet )
{ /* 将图的边存入数组ESet，并且初始化为最小堆 */
    Vertex V;
    PtrToAdjVNode W;
    int ECount;

    /* 将图的边存入数组ESet */
    ECount = 0;
    for ( V=0; V<Graph->Nv; V++ )
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( V < W->AdjV ) { /* 避免重复录入无向图的边，只收V1<V2的边 */
                ESet[ECount].V1 = V;
                ESet[ECount].V2 = W->AdjV;
                ESet[ECount++].Weight = W->Weight;
            }
    /* 初始化为最小堆 */
    for ( ECount=Graph->Ne/2; ECount>=0; ECount-- )
        PercDown( ESet, ECount, Graph->Ne );
}

int GetEdge( Edge ESet, int CurrentSize )
{ /* 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆 */

    /* 将最小边与当前堆的最后一个位置的边交换 */
    Swap( &ESet[0], &ESet[CurrentSize-1]);
    /* 将剩下的边继续调整成最小堆 */
    PercDown( ESet, 0, CurrentSize-1 );

    return CurrentSize-1; /* 返回最小边所在位置 */
}
/*-------------------- 最小堆定义结束 --------------------*/

int Kruskal( LGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
    WeightType TotalWeight;
    int ECount, NextEdge;
    SetType VSet; /* 顶点数组 */
    Edge ESet;    /* 边数组 */

    InitializeVSet( VSet, Graph->Nv ); /* 初始化顶点并查集 */
    ESet = (Edge)malloc( sizeof(struct ENode)*Graph->Ne );
    InitializeESet( Graph, ESet ); /* 初始化边的最小堆 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    TotalWeight = 0; /* 初始化权重和     */
    ECount = 0;      /* 初始化收录的边数 */

    NextEdge = Graph->Ne; /* 原始边集的规模 */
    while ( ECount < Graph->Nv-1 ) {  /* 当收集的边不足以构成树时 */
        NextEdge = GetEdge( ESet, NextEdge ); /* 从边集中得到最小边的位置 */
        if (NextEdge < 0) /* 边集已空 */
            break;
        /* 如果该边的加入不构成回路，即两端结点不属于同一连通集 */
        if ( CheckCycle( VSet, ESet[NextEdge].V1, ESet[NextEdge].V2 )==true ) {
            /* 将该边插入MST */
            InsertEdge( MST, ESet+NextEdge );
            TotalWeight += ESet[NextEdge].Weight; /* 累计权重 */
            ECount++; /* 生成树中边数加1 */
        }
    }
    if ( ECount < Graph->Nv-1 )
        TotalWeight = -1; /* 设置错误标记，表示生成树不存在 */

    return TotalWeight;
}

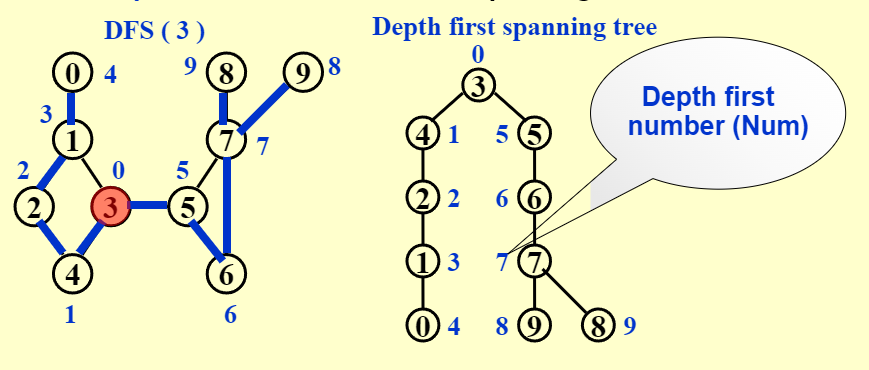
深度优先搜索 | DFS👀

void DFS ( Vertex V )  /* this is only a template */
{   
    visited[ V ] = true;  /* mark this vertex to avoid cycles */
    for ( each W adjacent to V )
        if ( !visited[ W ] )
            DFS( W );
} /* T = O( |E| + |V| ) as long as adjacency lists are used */

是先序遍历的一种推广

双连通 | Binconnectivity👀

  • 若一个图不是双连通的，那么将其删除后图不再连通的顶点叫做割点 (articulation point)
  • 若一个连通的无向图中的任一顶点删除后，剩下的图仍然连通 (即连通且无割点) ，则称其为双连通
  • 双连通分量 (biconnected component) 是极大的双连通子图
具有割点 C 和 D 的图

2023-02-01-13-24-22

  • Tarjan算法

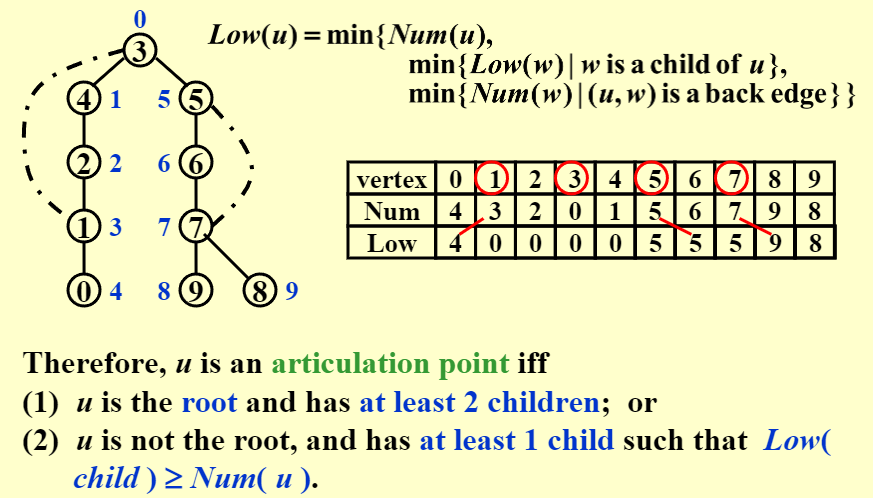
    对顶点的 Num 赋值例程 
    /* Assign Num and compute Parents */
void AssignNum(Vertex V)
{
    Vertex W;
    Num[V] = Counter ++;
    Visited[V] = True;
    for each W adjacent to V
        if(!Visited[W])
        {
            Parent[W] = V;
            AssignNum(W);
        }
}
    通过 DFS 建立的最小生成树

    2023-02-01-15-19-47
    2023-02-22-17-17-57

    back edge: ( \(u, v\) ) \(\notin\) tree and \(u\) (or \(v\) ) is an ancestor of \(v\) (or \(u\) )
    Note: If \(u\) is an ancestor of \(v\) , then Num( \(u\) ) < Num( \(v\) )

    • Num[v] 表示 v 第一次被访问的时间戳，即 DFS 时第几个被访问（从0开始）
    • 追溯值 low[x]
      • 对于图中从 x 到 y 的边 :
      • 如果 < x, y > 在树上，则 low[x] = min(Num[x], low[y])
      • 如果 < x, y > 不在树上，则 low[x] = min(Num[x], Num[y])
    • 寻找割点：
      • 如果 u 是 root，则 u 是割点当且仅当 u 有至少两个儿子
      • 如果 u 不是 root，则 u 是割点当且仅当存在一个儿子 v，满足 Num[u] \(\leq\) low[v]
    • 计算 Low 并检验是否割点 (忽略对根的检验) 
      /* Assign Low; also check for articulation points */
void AssignLow(Vertex V)
{
    Vertex W;

    Low[V] = Num[V];    /* Rule 1 */
    for each W adjacent to V
    {
        if(Num[W] > Num[V]) /* Forward edge */
        {
            AssignLow(W);
            if(Low[W] >= Num[V])
                printf("%v is an articulation point\n", v);
            Low[V] = Min(Low[V], Low[W]);
        }
        else if(Parent[V] != W) /* Back edge */
            Low[V] = Min(Low[V], Num[W]);   /* Rule 2 */

    }
}
    • 在一次 DFS 中对割点的检测 (忽略对根的检测)
      void FindArt(Vertex V)
{
    Vertex W;
    Visited[V] = True;
    Low[V] = Num[V] = Counter ++;
    for(each W adjacent to V)
    {
        if(!Visited[W])
        {
            Parent[W] = V;
            FindArt(W);
            if(Low[W] >= Num[V])
            {
                printf("%v is an articulation point\n", v);
            }
            Low[V] = Min(Low[V], Low[W]);
        }
        else
            if(Parent[V] != W)
            {
                Low[V] = Min(Low[V], Num[W]);
            }
    }
}

欧拉回路 & 欧拉路径👀

  • 欧拉路径 (Euler path | Euler tour) —— 一笔画 | 包含所有边的简单路径
    • 如果正好有两个度为奇数的顶点，欧拉路径就是可能的。必须从一个奇度的顶点开始 “画”
  • 欧拉回路 (Euler circuit) —— 一笔画并且结束点和起始点重合 | 包含所有边的简单环
    • 只有当图连通且每个顶点度为偶数，欧拉回路才有可能
  • 对无向图
    • 欧拉回路的判定: 图连通且所有顶点的度为偶数
    • 欧拉路径的判定: 图连通且有且仅有两个顶点的度数是奇数
  • 有向图
    • 欧拉回路的判定: 弱连通且所有顶点的出度等于入度
    • 欧拉路径的判定: 弱连通且有且仅有一个顶点的出度比入度大 1 及一个顶点的入度比出度大 1，其余顶点的出度等于入度

      弱连通 —— 将有向图的所有有向边替换为无向边得到的图是连通

  • DFS 遍历整张图即可求得路径
本文总阅读量: 次