Backtracking👀

约 474 个字 44 行代码预计阅读时间 2 分钟

Rationale

解决问题的一个可靠的方法是列出所有候选答案，检查每个答案，然后在所有或部分候选答案被检查之后，宣布确定的答案。
如果候选者有限且不是特别多的话，是可以在检查后确定答案的。
而 backtracking | 回溯法 使我们能够消除对大量候选子集的显式检查，同时仍然保证如果算法运行到终止时能找到答案。这种方法其实就是 pruning | 剪枝 思想。

basic idea

Suppose we have a partial solution \((x_1, x_2, \ldots, x_i)\), where each \(x_k \in S_k\) for \(1 \leq k \leq i < n\).
First we add \(x_{i+1} \in S_{i+1}\) and check if the new solution \((x_1, x_2, \ldots, x_{i+1})\) satisfies the constraints.
If the answer is “yes”, we continue to add the next \(x\), else we delete \(x_i\) and backtrack to the previous partial solution \((x_1, x_2, \ldots, x_{i-1})\).

DFS + purning = backtracking

下面，由一些经典问题来引入回溯法的基本思想。

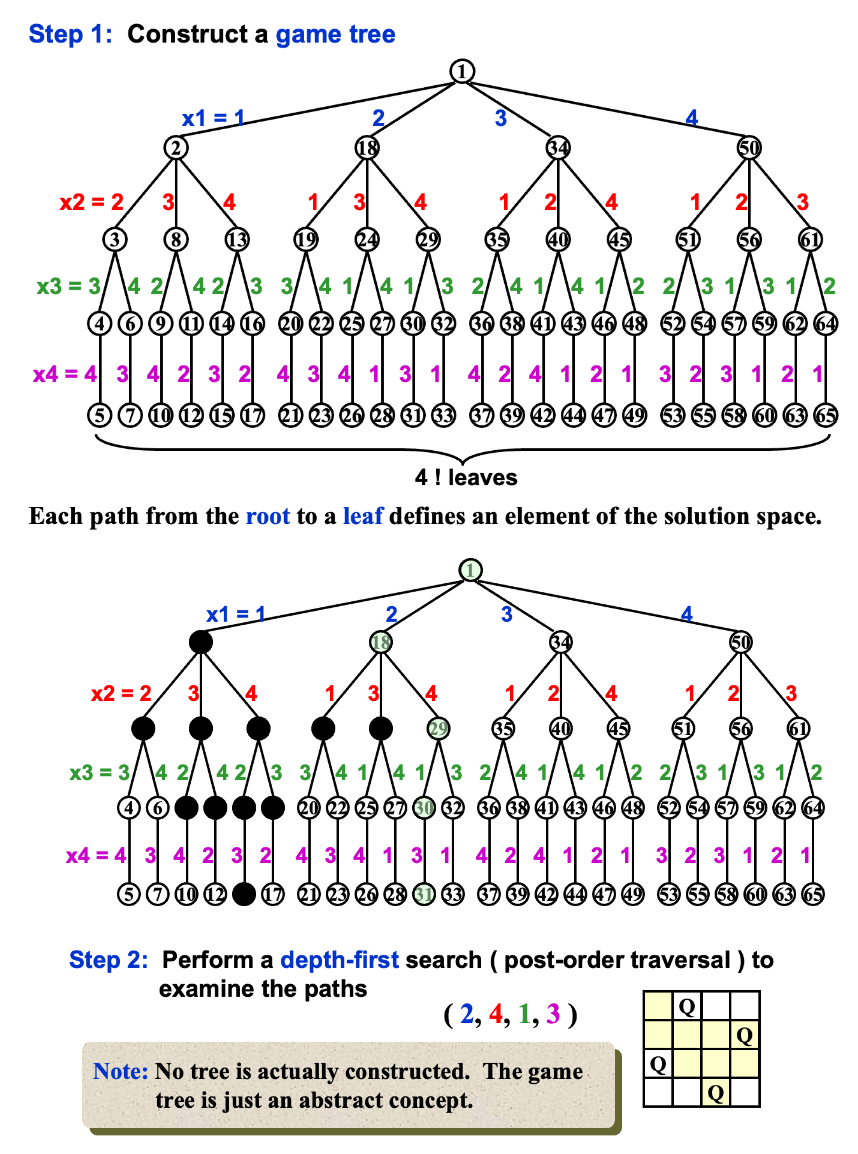
Eight Queens Problem👀

Problem

在 8 \(\times\) 8 格的国际象棋上摆放 8 个 queen，使其不能互相攻击
即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

例如其中一种解法如下：

该问题的 Constraints 如下：

\(S_i = \{1, 2, 3, 4, 5, 6, 7, 8\}\) for \(1 \leq i \leq 8\)
\(x_i \neq x_j\) if \(i \neq j\)
\((x_i - x_j) / (i - j) \neq \pm 1\) if \(i \neq j\)

其实，这个问题的 Constraints 第一个暗示解空间有 \(8^8\) 种可能

问题的第二条约束条件暗示了解空间的大小缩减为为 \(8!\) 种可能

以四皇后为例

Turnpike problem👀

For every d remaining in D, at least one of its endpoints is not determined
For maximum d remaining in D, at least one of its endpoints is a₀ or a_n-1

bool Reconstruct(DistType X[ ], DistSet D, int N, int left, int right)
{
    /* X[1]...X[left-1] and X[right+1]...X[N] are solved */
    bool Found = false;
    if ( Is_Empty( D ) ) return true; /* solved */
    D_max = Find_Max( D ); /* option 1：X[right] = D_max */
    /* check if |D_max-X[i]|D is true for all X[i]’s that have been solved */
    OK = Check( D_max, N, left, right ); /* pruning */
    if ( OK ) {
        /* add X[right] and update D */
        X[right] = D_max;
        for ( i=1; i<left; i++ )
            Delete( |X[right]-X[i]|, D);
        for ( i=right+1; i<=N; i++ )
            Delete( |X[right]-X[i]|, D);
        Found = Reconstruct ( X, D, N, left, right-1 );
        if ( !Found ) {
            /* if does not work, undo */
            for ( i=1; i<left; i++ )
                Insert( |X[right]-X[i]|, D);
            for ( i=right+1; i<=N; i++ )
                Insert( |X[right]-X[i]|, D);
        }
    } /* finish checking option 1 */
    if ( !Found ) { /* if option 1 does not work */
        /* option 2: X[left] = X[N]-D_max */
        OK = Check( X[N]-D_max, N, left, right );
        if ( OK ) {
            X[left] = X[N] – D_max;
            for ( i=1; i<left; i++ )
                Delete( |X[left]-X[i]|, D);
            for ( i=right+1; i<=N; i++ )
                Delete( |X[left]-X[i]|, D);
            Found = Reconstruct (X, D, N, left+1, right );
            if ( !Found ) {
                for ( i=1; i<left; i++ )
                    Insert( |X[left]-X[i]|, D);
                for ( i=right+1; i<=N; i++ )
                    Insert( |X[left]-X[i]|, D);
            }
        } /* finish checking option 2 */
    } /* finish checking all the options */
    return Found;
}

worst case: O(2ⁿ) (rare)
best case: O(n) (most instances)

Game - Tic-Tac-Toe👀

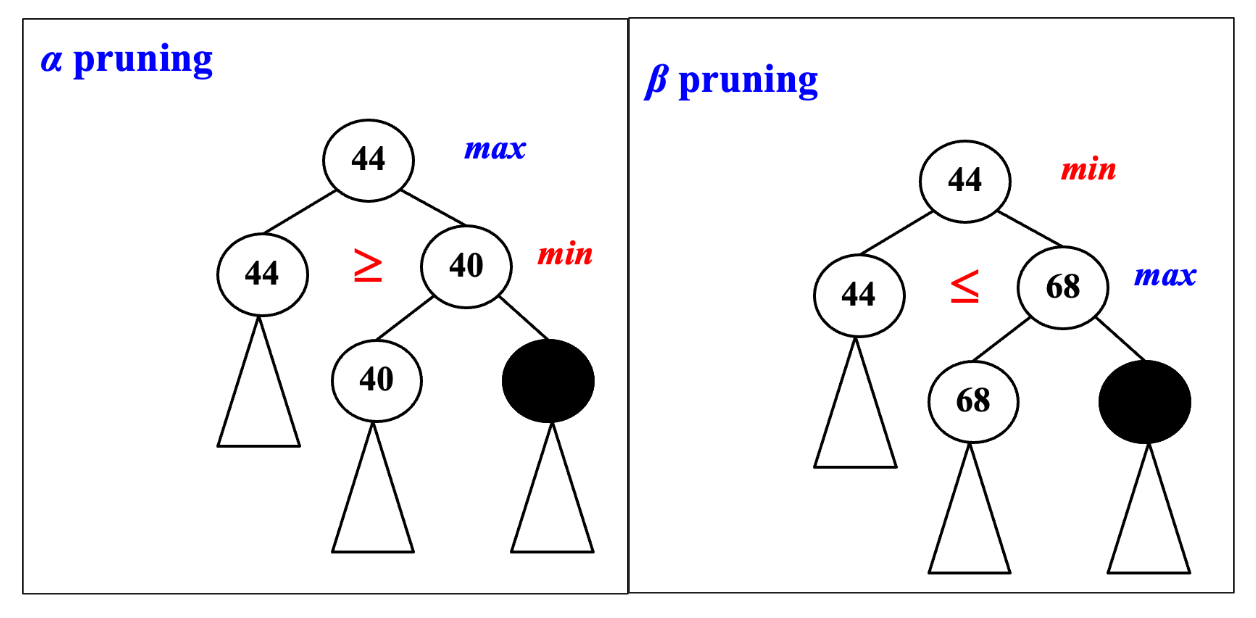
Pruning👀

不管树中黑色节点的值是多少，都没有意义

\(\alpha-\beta\) pruning: when both techniques are combined. In practice, it limits the searching to only \(O(\sqrt{N})\) nodes, where N is the size of the full game tree.

参考

最清晰易懂的MinMax算法和Alpha-Beta剪枝详解

本文总阅读量: 次